
Kakeya Needle Problem
 المؤلف:
Ball, W. W. R. and Coxeter, H. S. M
المؤلف:
Ball, W. W. R. and Coxeter, H. S. M
 المصدر:
Mathematical Recreations and Essays, 13th ed. New York: Dover
المصدر:
Mathematical Recreations and Essays, 13th ed. New York: Dover
 الجزء والصفحة:
...
الجزء والصفحة:
...
 10-2-2020
10-2-2020
 3445
3445
Kakeya Needle Problem
The Kakeya needle problems asks for the plane figure of least area in which a line segment of width 1 can be freely rotated (where translation of the segment is also allowed). Surprisingly, there is no minimum area (Besicovitch 1928). Another iterative construction which tends to as small an area as desired is called a Perron tree (Falconer 1990, Wells 1991).
When the figure is restricted to be convex, the smallest region is an equilateral triangle of unit height. Wells (1991) states that Kakeya discovered this, while Falconer (1990) attributes it to Pál.
If convexity is replaced by the weaker assumption of simply-connectedness, then the area can still be arbitrarily small, but if the set is required to be star-shaped, then 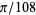 is a known lower bound (Cunningham 1965).
is a known lower bound (Cunningham 1965).
The smallest simple convex domain in which one can put a segment of length 1 which will coincide with itself when rotated by 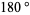 has area
has area
(OEIS A093823; Le Lionnais 1983).
REFERENCES:
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 99-101, 1987.
Besicovitch, A. S. "On Kakeya's Problem and a Similar One." Math. Z. 27, 312-320, 1928.
Besicovitch, A. S. "The Kakeya Problem." Amer. Math. Monthly 70, 697-706, 1963.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, pp. 81-82, 2003.
Cunningham, F. Jr. and Schoenberg, I. J. "On the Kakeya Constant." Canad. J. Math. 17, 946-956, 1965.
Falconer, K. J. The Geometry of Fractal Sets, 1st pbk. ed., with corrections. Cambridge, England: Cambridge University Press, 1990.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 24, 1983.
Littlewood, J. E. Littlewood's Miscellany. Cambridge, England: Cambridge University Press, p. 38, 1986.
Ogilvy, C. S. A Calculus Notebook. Boston, MA: Prindle, Weber, & Schmidt, 1968.
Ogilvy, C. S. Excursions in Geometry. New York: Dover, pp. 147-153, 1990.
Pál, J. "Ein Minimumproblem für Ovale." Math. Ann. 88, 311-319, 1921.
Sloane, N. J. A. Sequence A093823 in "The On-Line Encyclopedia of Integer Sequences."
Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, pp. 151-152, 1999.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 50-52, 1991.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 128-129, 1991.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


