

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Circle Packing
المؤلف:
Boll, D.
المصدر:
"Packing Results." http://www.frii.com/~dboll/packing.html
الجزء والصفحة:
...
5-2-2020
2783
Circle Packing
A circle packing is an arrangement of circles inside a given boundary such that no two overlap and some (or all) of them are mutually tangent. The generalization to spheres is called a sphere packing. Tessellations of regular polygons correspond to particular circle packings (Williams 1979, pp. 35-41). There is a well-developed theory of circle packing in the context of discrete conformal mapping (Stephenson).
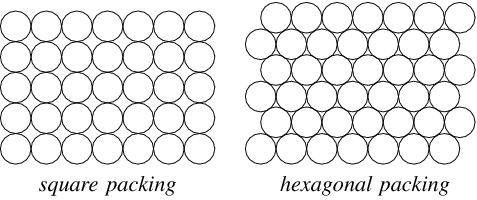
The densest packing of circles in the plane is the hexagonal lattice of the bee's honeycomb (right figure; Steinhaus 1999, p. 202), which has a packing density of
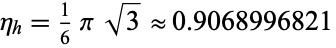 |
(1) |
(OEIS A093766; Wells 1986, p. 30). Gauss proved that the hexagonal lattice is the densest plane lattice packing, and in 1940, L. Fejes Tóth proved that the hexagonal lattice is indeed the densest of all possible plane packings.
Surprisingly, the circular disk is not the least economical region for packing the plane. The "worst" packing shape is not known, but among centrally symmetric plane regions, the conjectured candidate is the so-called smoothed octagon.
Wells (1991, pp. 30-31) considers the maximum size possible for 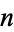 identical circles packed on the surface of a unit sphere.
identical circles packed on the surface of a unit sphere.
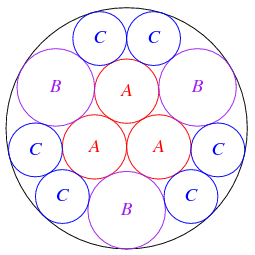
Using discrete conformal mapping, the radii of the circles in the above packing inside a unit circle can be determined as roots of the polynomial equations
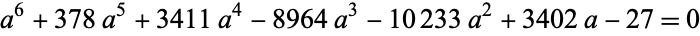 |
(2) |
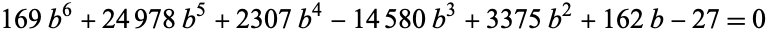 |
(3) |
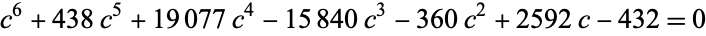 |
(4) |
with
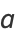 |
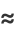 |
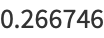 |
(5) |
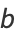 |
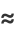 |
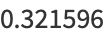 |
(6) |
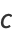 |
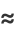 |
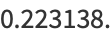 |
(7) |
The following table gives the packing densities 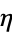 for the circle packings corresponding to the regular and semiregular plane tessellations (Williams 1979, p. 49).
for the circle packings corresponding to the regular and semiregular plane tessellations (Williams 1979, p. 49).
| tessellation | 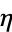 exact exact |
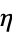 approx. approx. |
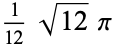 |
0.9069 | |
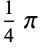 |
0.7854 | |
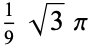 |
0.6046 | |
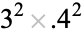 |
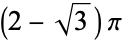 |
0.8418 |
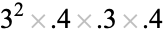 |
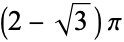 |
0.8418 |
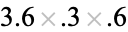 |
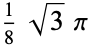 |
0.6802 |
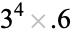 |
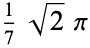 |
0.7773 |
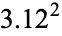 |
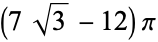 |
0.3907 |
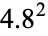 |
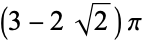 |
0.5390 |
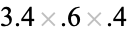 |
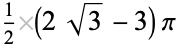 |
0.7290 |
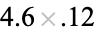 |
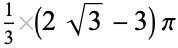 |
0.4860 |
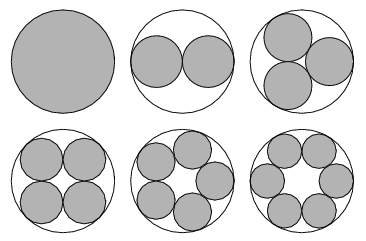
Solutions for the smallest diameter circles into which 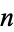 unit-diameter circles can be packed have been proved optimal for
unit-diameter circles can be packed have been proved optimal for 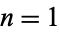 through 10 (Kravitz 1967). The best known results are summarized in the following table, and the first few cases are illustrated above (Friedman).
through 10 (Kravitz 1967). The best known results are summarized in the following table, and the first few cases are illustrated above (Friedman).
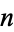 |
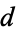 exact exact |
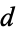 approx. approx. |
| 1 | 1 | 1.00000 |
| 2 | 2 | 2.00000 |
| 3 | 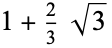 |
2.15470... |
| 4 | 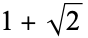 |
2.41421... |
| 5 | 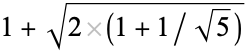 |
2.70130... |
| 6 | 3 | 3.00000 |
| 7 | 3 | 3.00000 |
| 8 | 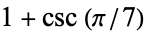 |
3.30476... |
| 9 | 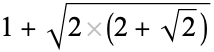 |
3.61312... |
| 10 | 3.82... | |
| 11 | ||
| 12 | 4.02... |

The following table gives the diameters 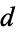 of circles giving the densest known packings of
of circles giving the densest known packings of 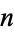 equal circles packed inside a unit square, the first few of which are illustrated above (Friedman). All
equal circles packed inside a unit square, the first few of which are illustrated above (Friedman). All 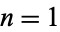 to 20 solutions (in addition to all solutions
to 20 solutions (in addition to all solutions 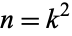 ) have been proved optimal (Friedman). Peikert (1994) uses a normalization in which the centers of
) have been proved optimal (Friedman). Peikert (1994) uses a normalization in which the centers of 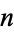 circles of diameter
circles of diameter 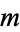 are packed into a square of side length 1. Friedman lets the circles have unit radius and gives the smallest square side length
are packed into a square of side length 1. Friedman lets the circles have unit radius and gives the smallest square side length 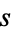 . A tabulation of analytic
. A tabulation of analytic 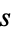 and diagrams for
and diagrams for 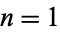 to 25 circles is given by Friedman. Coordinates for optimal packings are given by Nurmela and Östergård (1997).
to 25 circles is given by Friedman. Coordinates for optimal packings are given by Nurmela and Östergård (1997).
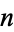 |
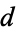 |
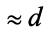 |
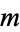 |
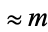 |
| 1 | 1 | 1.000000 | ||
| 2 | 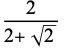 |
0.585786 | 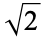 |
1.414214 |
| 3 | 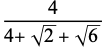 |
0.508666 | 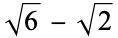 |
1.035276 |
| 4 | 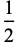 |
0.500000 | 1 | 1.000000 |
| 5 | 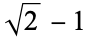 |
0.414214 | 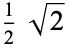 |
0.707107 |
| 6 | 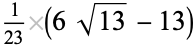 |
0.375361 | 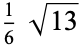 |
0.600925 |
| 7 | 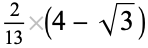 |
0.348915 | 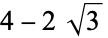 |
0.535898 |
| 8 | 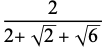 |
0.341081 | 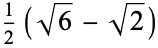 |
0.517638 |
| 9 | 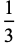 |
0.333333 | 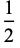 |
0.500000 |
| 10 | 0.296408 | 0.421280 |
The smallest square into which two unit circles, one of which is split into two pieces by a chord, can be packed is not known (Goldberg 1968, Ogilvy 1990).
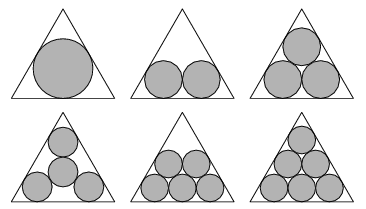
The best known packings of circles into an equilateral triangle are shown above for the first few cases (Friedman).
REFERENCES:
Boll, D. "Packing Results." http://www.frii.com/~dboll/packing.html
Bowers, P. L. and Stephenson, K. "Uniformizing Dessins and Belyĭ Maps via Circle Packing." Preprint.
Casado, L. G. and Szabó, P. G. "Equal Circle Packing in a Square." http://www.inf.u-szeged.hu/~pszabo/Packing_circles.html.
Collins, C. R. and Stephenson, K. "A Circle Packing Algorithm." Preprint.
Conway, J. H. and Sloane, N. J. A. Sphere Packings, Lattices, and Groups, 2nd ed. New York: Springer-Verlag, 1993.
Croft, H. T.; Falconer, K. J.; and Guy, R. K. Unsolved Problems in Geometry. New York: Springer-Verlag, 1991.
Donovan, J. "Packing Circles in Squares and Circles Page." http://home.att.net/~donovanhse/Packing/.
Eppstein, D. "Covering and Packing." http://www.ics.uci.edu/~eppstein/junkyard/cover.html.
Fejes Tóth, G. Lagerungen in der Ebene, auf der Kugel und in Raum, 2nd ed. Berlin: Springer-Verlag, 1972.
Folkman, J. H. and Graham, R. "A Packing Inequality for Compact Convex Subsets of the Plane." Canad. Math. Bull. 12, 745-752, 1969.
Friedman, E. "Circles in Circles." http://www.stetson.edu/~efriedma/cirincir/.
Friedman, E. "Squares in Circles." http://www.stetson.edu/~efriedma/squincir/.
Friedman, E. "Triangles in Circles." http://www.stetson.edu/~efriedma/triincir/.
Gardner, M. "Mathematical Games: The Diverse Pleasures of Circles That Are Tangent to One Another." Sci. Amer. 240, 18-28, Jan. 1979.
Gardner, M. "Tangent Circles." Ch. 10 in Fractal Music, Hypercards, and More Mathematical Recreations from Scientific American Magazine. New York: W. H. Freeman, pp. 149-166, 1992.
Goldberg, M. "Problem E1924." Amer. Math. Monthly 75, 195, 1968.
Goldberg, M. "The Packing of Equal Circles in a Square." Math. Mag. 43, 24-30, 1970.
Goldberg, M. "Packing of 14, 16, 17, and 20 Circles in a Circle." Math. Mag. 44, 134-139, 1971.
Graham, R. L. and Luboachevsky, B. D. "Repeated Patterns of Dense Packings of Equal Disks in a Square." Electronic J. Combinatorics 3, No. 1, R16, 1-17, 1996. http://www.combinatorics.org/Volume_3/Abstracts/v3i1r16.html.
Graham, R. L.; Luboachevsky, B. D.; Nurmela, K. J.; and Östergård, P. R. J. "Dense Packings of Congruent Circles in a Circle." Discrete Mat. 181, 139-154, 1998.
Hannachi, N. "Kissing Circles." http://perso.wanadoo.fr/math-a-mater/pack/packingcircle.htm.
Kravitz, S. "Packing Cylinders into Cylindrical Containers." Math. Mag. 40, 65-70, 1967.
Likos, C. N. and Henley, C. L. "Complex Alloy Phases for Binary Hard-Disc Mixtures." Philos. Mag. B 68, 85-113, 1993.
Maranas, C. D.; Floudas, C. A.; and Pardalos, P. M. "New Results in the Packing of Equal Circles in a Square." Disc. Math. 142, 287-293, 1995.
McCaughan, F. "Circle Packings." http://www.pmms.cam.ac.uk/~gjm11/cpacking/info.html.
Molland, M. and Payan, Charles. "A Better Packing of Ten Equal Circles in a Square." Discrete Math. 84, 303-305, 1990.
Nurmela, K. J. and Östergård, P. R. J. "Packing Up to 50 Equal Circles in a Square." Disc. Comput. Geom. 18, 111-120, 1997.
Nurmela, K. J. and Östergård, P. R. J. packings/square/. http://www.tcs.hut.fi/packings/square/
Ogilvy, C. S. Excursions in Geometry. New York: Dover, p. 145, 1990.
Peikert, R. "Packing of Equal Circles in a Square." http://www.inf.ethz.ch/~peikert/personal/CirclePackings/.
Peikert, R. "Dichteste Packungen von gleichen Kreisen in einem Quadrat." Elem. Math. 49, 16-26, 1994.
Peikert, R.; Würtz, D.; Monagan, M.; and de Groot, C. "Packing Circles in a Square: A Review and New Results." In System Modelling and Optimization, Proceedings of the Fifteenth IFIP Conference Held at the University of Zürich, September 2-6, 1991 (Ed. P. Kall). Berlin: Springer-Verlag, pp. 45-54, 1992.
Reis, G. E. "Dense Packing of Equal Circle within a Circle." Math. Mag. 48, 33-37, 1975.
Schaer, J. "The Densest Packing of Nine Circles in a Square." Can. Math. Bul. 8, 273-277, 1965.
Schaer, J. "The Densest Packing of Ten Equal Circles in a Square." Math. Mag. 44, 139-140, 1971.
Sloane, N. J. A. Sequence A093766 in "The On-Line Encyclopedia of Integer Sequences."
Specht, E. "The Best Known Packings of Equal Circles in the Unit Square." http://hydra.nat.uni-magdeburg.de/packing/csq.html.
Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, p. 202, 1999.
Stephenson, K. "Circle Packing." http://www.math.utk.edu/~kens/#Packing.
Stephenson, K. "Circle Packing Bibliography as of April 1999." http://www.math.utk.edu/~kens/CP-bib.ps.
Stephenson, K. "Circle Packings in the Approximation of Conformal Mappings." Bull. Amer. Math. Soc. 23, 407-416, 1990.
Stephenson, K. "A Probabilistic Proof of Thurston's Conjecture on Circle Packings." Rend. Sem. Math. Fis. Milano 66, 201-291, 1998.
Stephenson, K. Introduction to Circle Packing : The Theory of Discrete Analytic Functions. New York: Cambridge University Press, 2005.
Valette, G. "A Better Packing of Ten Equal Circles in a Square." Discrete Math. 76, 57-59, 1989.
van Dam, E.; den Hertog, D.; Husslage, B.; and Rennen, G. "Maximin Designs (Dimensions: 2)." Mar. 31, 2006. http://www.spacefillingdesigns.nl/.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 30, 1986.
Williams, R. "Circle Packings, Plane Tessellations, and Networks." §2.3 in The Geometrical Foundation of Natural Structure: A Source Book of Design. New York: Dover, pp. 34-47, 1979.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, pp. 350 and 987, 2002.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















