تاريخ الرياضيات
الاعداد و نظريتها
تاريخ التحليل
تار يخ الجبر
الهندسة و التبلوجي
الرياضيات في الحضارات المختلفة
العربية
اليونانية
البابلية
الصينية
المايا
المصرية
الهندية
الرياضيات المتقطعة
المنطق
اسس الرياضيات
فلسفة الرياضيات
مواضيع عامة في المنطق
الجبر
الجبر الخطي
الجبر المجرد
الجبر البولياني
مواضيع عامة في الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
الهندسة المستوية
الهندسة غير المستوية
مواضيع عامة في الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
معادلات تفاضلية
معادلات تكاملية
مواضيع عامة في المعادلات
التحليل
التحليل العددي
التحليل العقدي
التحليل الدالي
مواضيع عامة في التحليل
التحليل الحقيقي
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
500AD
500-1499
1000to1499
1500to1599
1600to1649
1650to1699
1700to1749
1750to1779
1780to1799
1800to1819
1820to1829
1830to1839
1840to1849
1850to1859
1860to1864
1865to1869
1870to1874
1875to1879
1880to1884
1885to1889
1890to1894
1895to1899
1900to1904
1905to1909
1910to1914
1915to1919
1920to1924
1925to1929
1930to1939
1940to the present
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان
Lévy Constant
المؤلف:
Corless, R. M
المصدر:
"Continued Fractions and Chaos." Amer. Math. Monthly 99
الجزء والصفحة:
...
31-1-2020
2271
+
-
20
Lévy Constant
The nth root of the denominator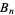 
of the 
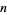th convergent 
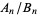of a number 
tends to a constant
 |
 |
 |
(1) |
 |
 |
 |
(2) |
 |
 |
 |
(3) |
(OEIS A086702) for all but a set of 
of measure zero (Lévy 1936, Lehmer 1939), where
 |
 |
 |
(4) |
 |
 |
 |
(5) |
Some care is needed in terminology and notation related to this constant. Most authors call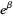 
"Lévy's constant" (e.g., Le Lionnais 1983, p. 51; Sloane) and some (S. Plouffe) call 
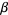the "Khinchin-Lévy constant." Other authors refer to 
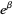(e.g., Finch 2003, p. 60) or 
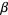(e.g., Wu 2008) without specifically naming the expression in question.
Taking the multiplicative inverse of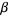 
gives another related constant,
 |
 |
 |
(6) |
 |
 |
 |
(7) |
(OEIS A089729).
Corless (1992) showed that
 |
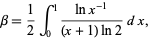(8) |
with an analogous formula for Khinchin's constant.
The Lévy Constant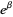 
is related to Lochs' constant 
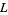by
 |
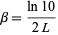(9) |
or
 |
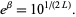(10) |
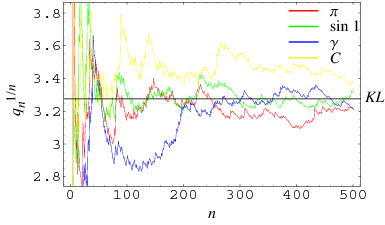
The plot above shows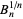 
for the first 500 terms in the continued fractions of 
, 
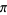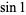, the Euler-Mascheroni constant 
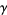, and the Copeland-Erdős constant 
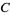. Interestingly, the shape of the curves is almost identical to the corresponding curves for Khinchin's constant
REFERENCES:
Corless, R. M. "Continued Fractions and Chaos." Amer. Math. Monthly 99, 203-215, 1992.
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 60 and 156, 2003.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 51, 1983.
Lehmer, D. H. "Note on an Absolute Constant of Khintchine." Amer. Math. Monthly 46, 148-152, 1939.
Lévy, P. "Sur le développement en fraction continue d'un nombre choisi au hasard." Compositio Math. 3, 286-303, 1936. Reprinted in Œuvres de Paul Lévy, Vol. 6. Paris: Gauthier-Villars, pp. 285-302, 1980.
Rockett, A. M. and Szüsz, P. "The Khintchine-Lévy Theorem for {B, _, n}, n]" src="http://mathworld.wolfram.com/images/equations/LevyConstant/Inline39.gif" style="height:27px; width:33px" />." §5.9 in Continued Fractions. New York: World Scientific, pp. 163-166, 1992.
Sloane, N. J. A. Sequences A086702 and A089729 in "The On-Line Encyclopedia of Integer Sequences."
Wu. J. "An Iterated Logarithm Law Related to Decimal and Continued Fraction Expansions." Monatsh. f. Math. 153, 83-87, 2008.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
الآخبار الصحية
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
