e Digits

The constant e with decimal expansion

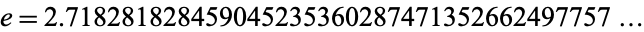(OEIS A001113) can be computed to  digits of precision in 10 CPU-minutes on modern hardware.

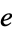 was computed to  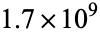digits by P. Demichel, and the first  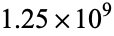have been verified by X. Gourdon on Nov. 21, 1999 (Plouffe).  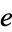was computed to  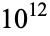decimal digits by S. Kondo on Jul. 5, 2010 (Yee).

The Earls sequence (starting position of 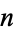 copies of the digit 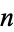) for 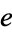 is given for 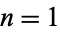, 2, ... by 2, 252, 1361, 11806, 210482, 9030286, 3548262, 141850388, 1290227011, ... (OEIS A224828).

The starting positions of the first occurrence of 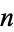 in the decimal expansion of  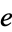(including the initial 2 and counting it as the first digit) are 14, 3, 1, 18, 11, 12, 21, 2, ... (OEIS A088576).

Scanning the decimal expansion of 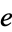 until all 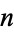-digit numbers have occurred, the last 1-, 2-, ... digit numbers appearing are 6, 12, 548, 1769, 92994, ... (OEIS A036900), which end at digits 21, 372, 8092, 102128, ... (OEIS A036904).

The digit sequence 0123456789 does not occur in the first 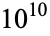 digits of , but 9876543210 does, starting at position 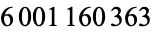 (E. Weisstein, Jul. 22, 2013).

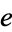-constant primes (i.e., e-primes) occur at 1, 3, 7, 85, 1781, 2780, 112280, 155025, ... (OEIS A64118) decimal digits.

It is not known if  is normal, but the following table giving the counts of digits in the first 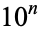 terms shows that the decimal digits are very uniformly distributed up to at least .

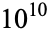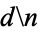	OEIS	10	100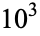
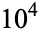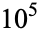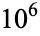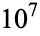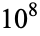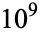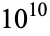0	A000000	0	5	100	974	9885	99425	998678	9999138	100004425	1000024802
1	A000000	2	6	96	989	10264	100132	1000577	10004438	99982926	999989229
2	A000000	2	12	97	1004	9855	99845	999156	9998876	99999168	999997938
3	A000000	0	8	109	1008	10035	100228	1001716	10005176	100002498	999982936
4	A000000	1	11	100	982	10039	100389	1000307	9998285	100018922	1000026506
5	A000000	0	13	85	992	10034	100087	999903	9998042	100003884	999967300
6	A000000	0	12	99	1079	10183	100479	998869	10000158	99987241	999931170
7	A000000	1	16	99	1008	9875	99910	1000813	9998342	99997536	1000013049
8	A000000	4	7	103	996	9967	99814	999703	10000336	100005348	1000074277
9	A000000	0	10	112	968	9863	99691	1000278	9997209	99998052	999992793

REFERENCES:

Sloane, N. J. A. Sequences A001113/M1727, A036900, A036904, A064118, A088576, and A224828 in "The On-Line Encyclopedia of Integer Sequences."

Yee, A. J. "y-cruncher - A Multi-Threaded Pi-Program." http://www.numberworld.org/y-cruncher/.