
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-12-2020
Date: 8-7-2020
Date: 30-1-2021
|
Petersson considered the absolutely converging Dirichlet L-series
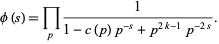 |
(1) |
Writing the denominator as
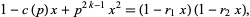 |
(2) |
where
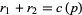 |
(3) |
and
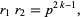 |
(4) |
Petersson conjectured that 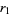 and
and 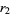 are always complex conjugate, which implies
are always complex conjugate, which implies
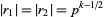 |
(5) |
and
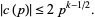 |
(6) |
This conjecture was proven by Deligne (1974), which also proved the tau conjecture as a special case. Deligne was awarded the Fields medal for his proof.
REFERENCES:
Apostol, T. M. Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, p. 140, 1997.
Deligne, P. "La conjecture de Weil. I." Inst. Hautes Études Sci. Publ. Math. 43, 273-307, 1974.
Deligne, P. "La conjecture de Weil. II." Inst. Hautes Études Sci. Publ. Math. 52, 137-252, 1980.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|