It is possible to perform multiplication of large numbers in (many) fewer operations than the usual brute-force technique of "long multiplication." As discovered by Karatsuba (Karatsuba and Ofman 1962), multiplication of two 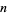-digit numbers can be done with a bit complexity of less than  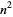using identities of the form

(1)

Proceeding recursively then gives bit complexity 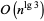, where  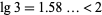(Borwein et al. 1989). The best known bound is  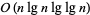steps for  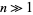(Schönhage and Strassen 1971, Knuth 1998). However, this algorithm is difficult to implement, but a procedure based on the fast Fourier transform is straightforward to implement and gives bit complexity  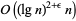(Brigham 1974, Borodin and Munro 1975, Borwein et al. 1989, Knuth 1998).

As a concrete example, consider multiplication of two numbers each just two "digits" long in base ,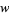

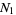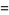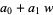			(2)
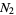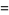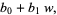			(3)

then their product is

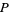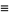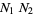			(4)
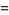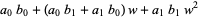			(5)
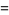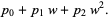			(6)

Instead of evaluating products of individual digits, now write

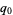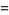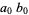			(7)
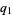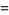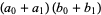			(8)
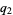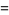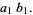			(9)

The key term is 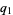, which can be expanded, regrouped, and written in terms of the  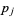as

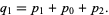(10)

However, since 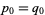, and 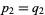, it immediately follows that

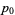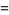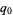			(11)
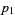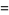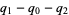			(12)
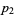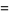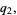			(13)

so the three "digits" of 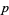 have been evaluated using three multiplications rather than four. The technique can be generalized to multidigit numbers, with the trade-off being that more additions and subtractions are required.

Now consider four-"digit" numbers

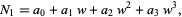(14)

which can be written as a two-"digit" number represented in the base ,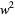

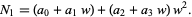(15)

The "digits" in the new base are now

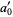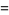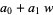			(16)
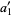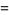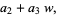			(17)

and the Karatsuba algorithm can be applied to 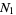 and 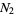 in this form. Therefore, the Karatsuba algorithm is not restricted to multiplying two-digit numbers, but more generally expresses the multiplication of two numbers in terms of multiplications of numbers of half the size. The asymptotic speed the algorithm obtains by recursive application to the smaller required subproducts is  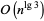(Knuth 1998).

When this technique is recursively applied to multidigit numbers, a point is reached in the recursion when the overhead of additions and subtractions makes it more efficient to use the usual 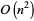 multiplication algorithm to evaluate the partial products. The most efficient overall method therefore relies on a combination of Karatsuba and conventional multiplication.

REFERENCES:

Bernstein, D. J. "Fast Multiplication and Its Applications." To appear in Alg. Number Th. http://cr.yp.to/lineartime/multapps-20041007.pdf.

Borodin, A. and Munro, I. The Computational Complexity of Algebraic and Numeric Problems. New York: American Elsevier, 1975.

Borwein, J. M.; Borwein, P. B.; and Bailey, D. H. "Ramanujan, Modular Equations, and Approximations to Pi, or How to Compute One Billion Digits of Pi." Amer. Math. Monthly 96, 201-219, 1989.

Brigham, E. O. The Fast Fourier Transform. Englewood Cliffs, NJ: Prentice-Hall, 1974.

Brigham, E. O. Fast Fourier Transform and Applications. Englewood Cliffs, NJ: Prentice-Hall, 1988.

Cook, S. A. On the Minimum Computation Time of Functions. Ph.D. Thesis. Cambridge, MA: Harvard University, pp. 51-77, 1966.

Hollerbach, U. "Fast Multiplication & Division of Very Large Numbers." sci.math.research posting, Jan. 23, 1996.

Karatsuba, A. and Ofman, Yu. "Multiplication of Many-Digital Numbers by Automatic Computers." Doklady Akad. Nauk SSSR 145, 293-294, 1962. Translation in Physics-Doklady 7, 595-596, 1963.

Knuth, D. E. The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 3rd ed. Reading, MA: Addison-Wesley, pp. 278-286, 1998.

Schönhage, A. and Strassen, V. "Schnelle Multiplikation Grosser Zahlen." Computing 7, 281-292, 1971.

Toom, A. L. "The Complexity of a Scheme of Functional Elements Simulating the Multiplication of Integers." Dokl. Akad. Nauk SSSR 150, 496-498, 1963. English translation in Soviet Mathematics 3, 714-716, 1963.

Zuras, D. "More on Squaring and Multiplying Large Integers." IEEE Trans. Comput. 43, 899-908, 1994.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الإعلام يشارك في الاجتماع التحضيري لمناقشة الخطة الإعلامية لزيارة عاشوراء

بحضور متوليها الشرعي.. العتبة العباسية المقدسة تواصل إقامة المجالس الحسينية لإحياء شهر المحرم

قسم الشؤون الفكرية يطلق برنامجه التبليغي في أكثر من 20 دولة إفريقية

شعبتا الخطابة النسوية والتوجيه الديني تواصلان إقامة المجالس الحسينية في مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

دراسة تحذر.. اضطراب نوم بسيط قد يسبب الموت المبكر ؟

الاستحمام بالماء الساخن.. راحة مؤقتة وأضرار دائمة للبشرة

ماذا يحدث للجسم عند تخطي وجبة الإفطار؟

المزيد

الآخبار التكنلوجية

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

السد الصيني العملاق يعيق دوران الأرض ويغيّر شكلها ؟

السعودية تطلق 10 تجارب علمية إلى محطة الفضاء الدولية

المزيد