المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Mott Polynomial |
 1499
 05:28 مساءً
date: 21-9-2019 |
Author : Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. 
Book or Source : Higher Transcendental Functions, Vol. 3. New York: Krieger 
Page and Part : ...|
Read More
Date: 21-8-2019
1560
Date: 23-8-2019
1430
Date: 21-8-2018
1793
|
Polynomials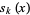 
which form the Sheffer sequence for
 |
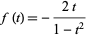(1) |
and have exponential generating function
![sum_(k=0)^infty(s_k(x))/(k!)t^k=exp[(x(1-sqrt(1+t^2)))/t].](http://mathworld.wolfram.com/images/equations/MottPolynomial/NumberedEquation2.gif) |
(2) |
The first few are
 |
 |
 |
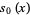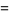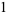(3) |
 |
 |
 |
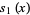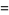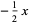(4) |
 |
 |
 |
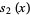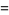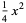(5) |
 |
 |
 |
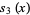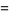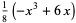(6) |
 |
 |
 |
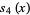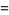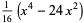(7) |
 |
 |
 |
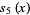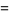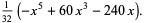(8) |
REFERENCES:
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Higher Transcendental Functions, Vol. 3. New York: Krieger, p. 251, 1981.
Roman, S. The Umbral Calculus. New York: Academic Press, 1984.
|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
المجمع العلميّ يُواصل عقد جلسات تعليميّة في فنون الإقراء لطلبة العلوم الدينيّة في النجف الأشرف
|
|
|
