المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Brahmagupta Polynomial |
 1341
 05:08 مساءً
date: 17-9-2019 |
Author : Suryanarayan, E. R 
Book or Source : "The Brahmagupta Polynomials." Fib. Quart. 34 
Page and Part : 30-39|
Read More
Date: 17-9-2019
1543
Date: 29-4-2018
2217
Date: 20-6-2019
1209
|
One of the polynomials obtained by taking powers of the Brahmagupta matrix. They satisfy the recurrence relation
 |
 |
 |
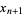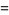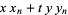(1) |
 |
 |
 |
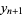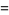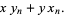(2) |
A list of many others is given by Suryanarayan (1996). Explicitly,
 |
 |
 |
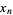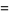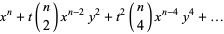(3) |
 |
 |
 |
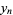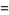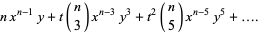(4) |
The Brahmagupta polynomials satisfy
 |
 |
 |
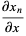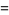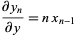(5) |
 |
 |
 |
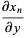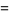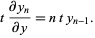(6) |
The first few polynomials are
 |
 |
 |
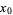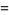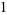(7) |
 |
 |
 |
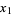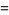(8) |
 |
 |
 |
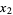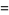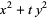(9) |
 |
 |
 |
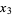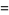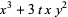(10) |
 |
 |
 |
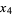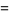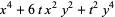(11) |
and
 |
 |
 |
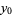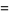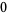(12) |
 |
 |
 |
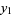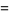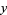(13) |
 |
 |
 |
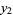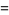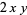(14) |
 |
 |
 |
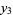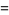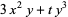(15) |
 |
 |
 |
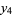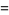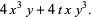(16) |
Taking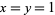 
and 
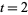gives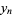 
equal to the Pell numbers and 
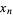equal to half the Pell-Lucas numbers. The Brahmagupta polynomials are related to the Morgan-Voyce polynomials, but the relationship given by Suryanarayan (1996) is incorrect.
REFERENCES:
Suryanarayan, E. R. "The Brahmagupta Polynomials." Fib. Quart. 34, 30-39, 1996.
|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
|
|
|
