


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-5-2019
Date:
Date: 23-6-2019
|
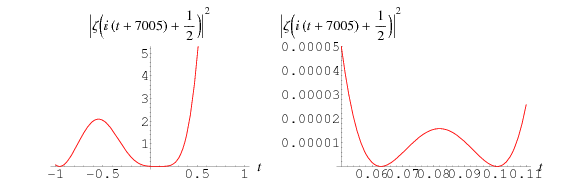
The appearance of nontrivial zeros (i.e., those along the critical strip with ![R[z]=1/2](http://mathworld.wolfram.com/images/equations/LehmersPhenomenon/Inline1.gif) ) of the Riemann zeta function
) of the Riemann zeta function 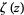 very close together. An example is the pair of zeros
very close together. An example is the pair of zeros 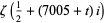 given by
given by 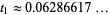 and
and 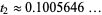 , illustrated above in the plot of
, illustrated above in the plot of 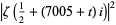 . This corresponds to the region near Gram point
. This corresponds to the region near Gram point 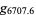 (Lehmer 1956; Edwards 2001, p. 178).
(Lehmer 1956; Edwards 2001, p. 178).
Let 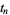 be the
be the 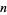 th nontrivial root of
th nontrivial root of 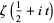 , and consider the local extrema of
, and consider the local extrema of 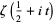 . Then the values of
. Then the values of 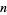 after which the absolute value of the local extremum between
after which the absolute value of the local extremum between 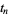 and
and 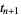 decreases are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 26, 27, 29, 30, ... (OEIS A114886).
decreases are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 26, 27, 29, 30, ... (OEIS A114886).
REFERENCES:
Csordas, G.; Odlyzko, A. M.; Smith, W.; and Varga, R. S. "A New Lehmer Pair of Zeros and a New Lower Bound for the de Bruijn-Newman Constant." Elec. Trans. Numer. Analysis 1, 104-111, 1993.
Csordas, G.; Smith, W.; and Varga, R. S. "Lehmer Pairs of Zeros, the de Bruijn-Newman Constant and the Riemann Hypothesis." Constr. Approx. 10, 107-129, 1994.
Csordas, G.; Smith, W.; and Varga, R. S. "Lehmer Pairs of Zeros and the Riemann 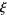 -Function." In Mathematics of Computation 1943-1993: A Half-Century of Computational Mathematics (Vancouver, BC, 1993). Proc. Sympos. Appl. Math. 48, 553-556, 1994.
-Function." In Mathematics of Computation 1943-1993: A Half-Century of Computational Mathematics (Vancouver, BC, 1993). Proc. Sympos. Appl. Math. 48, 553-556, 1994.
Edwards, H. M. "Lehmer's Phenomenon." §8.3 in Riemann's Zeta Function. New York: Dover, pp. 175-179, 2001.
Lehmer, D. H. "On the Roots of the Riemann Zeta-Function." Acta Math. 95, 291-298, 1956.
Sloane, N. J. A. Sequence A114886 in "The On-Line Encyclopedia of Integer Sequences."
Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 357-358, 1991.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقدم دعوة إلى كلية مزايا الجامعة للمشاركة في حفل التخرج المركزي الخامس
|
|
|