


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-9-2019
Date: 12-9-2019
Date: 31-7-2019
|
A sequence of approximations 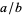 to
to 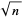 can be derived by factoring
can be derived by factoring
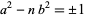 |
(1) |
(where 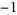 is possible only if
is possible only if 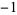 is a quadratic residue of
is a quadratic residue of 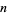 ). Then
). Then
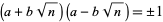 |
(2) |
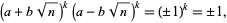 |
(3) |
and
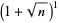 |
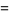 |
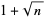 |
(4) |
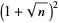 |
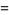 |
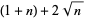 |
(5) |
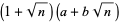 |
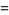 |
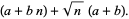 |
(6) |
Therefore, 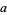 and
and 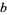 are given by the recurrence relations
are given by the recurrence relations
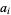 |
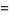 |
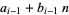 |
(7) |
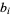 |
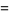 |
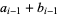 |
(8) |
with 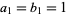 . The error obtained using this method is
. The error obtained using this method is
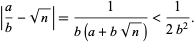 |
(9) |
The first few approximants to 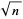 are therefore given by
are therefore given by
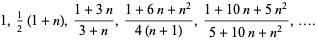 |
(10) |
This algorithm is sometimes known as the Bhaskara-Brouncker algorithm, and the approximants are precisely those obtained by taking successive convergents to the continued fraction of 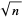 . The fact that if
. The fact that if 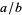 is an approximation to
is an approximation to 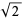 , then
, then 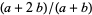 is a better one (the
is a better one (the 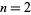 case) was known to Theon of Smyrna in the second century AD (Wells 1986, p. 35).
case) was known to Theon of Smyrna in the second century AD (Wells 1986, p. 35).
Another general technique for deriving this sequence, known as Newton's iteration, is obtained by letting 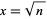 . Then
. Then 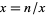 , so the sequence
, so the sequence
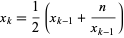 |
(11) |
converges quadratically to the root. The first few approximants to 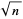 are therefore given by
are therefore given by
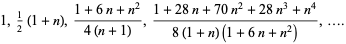 |
(12) |
Wolfram's iteration provides a method for finding square roots of integers using the binary representation.
REFERENCES:
Flannery, S. and Flannery, D. In Code: A Mathematical Journey. London: Profile Books, p. 132, 2000.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 34-35, 1986.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 1168, 2002.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|