


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-6-2019
Date: 21-9-2019
Date: 25-9-2019
|
 |
 |
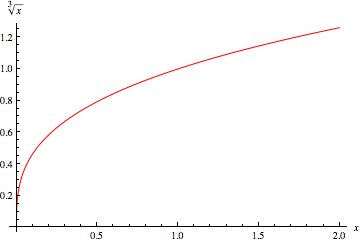
Given a number 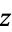 , the cube root of
, the cube root of 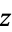 , denoted
, denoted ![RadicalBox[z, 3]](http://mathworld.wolfram.com/images/equations/CubeRoot/Inline3.gif) or
or 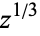 (
(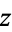 to the 1/3 power), is a number
to the 1/3 power), is a number 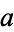 such that
such that 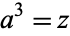 . The cube root is therefore an nth root with
. The cube root is therefore an nth root with 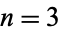 . Every real number has a unique real cube root, and every nonzero complex number has three distinct cube roots.
. Every real number has a unique real cube root, and every nonzero complex number has three distinct cube roots.
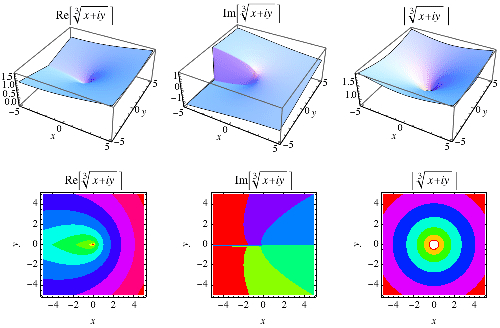
The schoolbook definition of the cube root of a negative number is 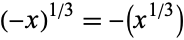 . However, extension of the cube root into the complex plane gives a branch cut along the negative real axis for the principal value of the cube root as illustrated above. By convention, "the" (principal) cube root is therefore a complex number with positive imaginary part. As a result, the Wolfram Language and other symbolic algebra languages and programs that return results valid over the entire complex plane therefore return complex results for
. However, extension of the cube root into the complex plane gives a branch cut along the negative real axis for the principal value of the cube root as illustrated above. By convention, "the" (principal) cube root is therefore a complex number with positive imaginary part. As a result, the Wolfram Language and other symbolic algebra languages and programs that return results valid over the entire complex plane therefore return complex results for 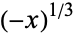 . For example, in the Wolfram Language, ComplexExpand[(-1)^(1/3)] gives the result
. For example, in the Wolfram Language, ComplexExpand[(-1)^(1/3)] gives the result 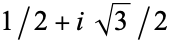 .
.
When considering a positive real number 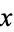 , the Wolfram Language function CubeRoot[x], which is equivalent to Surd[x, 3], may be used to return the real cube root.
, the Wolfram Language function CubeRoot[x], which is equivalent to Surd[x, 3], may be used to return the real cube root.
The cube root of a number 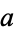 can be computed using Newton's method by iteratively applying
can be computed using Newton's method by iteratively applying
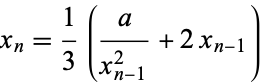 |
for some real starting value 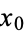 .
.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|