


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-7-2019
Date: 29-9-2018
Date: 15-5-2018
|
A 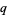 -analog, also called a
-analog, also called a 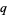 -extension or
-extension or 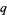 -generalization, is a mathematical expression parameterized by a quantity
-generalization, is a mathematical expression parameterized by a quantity 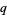 that generalizes a known expression and reduces to the known expression in the limit
that generalizes a known expression and reduces to the known expression in the limit 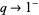 . There are
. There are 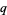 -analogs of the factorial, binomial coefficient, derivative, integral, Fibonacci numbers, and so on. Koornwinder, Suslov, and Bustoz, have even managed some kind of
-analogs of the factorial, binomial coefficient, derivative, integral, Fibonacci numbers, and so on. Koornwinder, Suslov, and Bustoz, have even managed some kind of 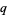 -Fourier analysis. Note that while European writers generally prefer the British spelling "
-Fourier analysis. Note that while European writers generally prefer the British spelling "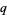 -analogue" (Koekoek and Swarttouw 1998, p. 7; Koepf 1998, p. 26), American authors prefer the shorter "
-analogue" (Koekoek and Swarttouw 1998, p. 7; Koepf 1998, p. 26), American authors prefer the shorter "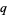 -analog" (Andrews et al. 1999, pp. 490 and 496). To avoid this ambiguity (as well as the pitfall that there are sometimes more than just a single
-analog" (Andrews et al. 1999, pp. 490 and 496). To avoid this ambiguity (as well as the pitfall that there are sometimes more than just a single 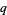 -analog), the term
-analog), the term 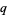 -extension (Andrews et al. 1999, pp. 483, 485, 487, etc.) may be preferable.
-extension (Andrews et al. 1999, pp. 483, 485, 487, etc.) may be preferable.
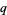 -analogs are based on the observation that
-analogs are based on the observation that
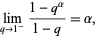 |
(1) |
and the quantity 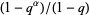 is sometimes written
is sometimes written ![[alpha]](http://mathworld.wolfram.com/images/equations/q-Analog/Inline14.gif) (Koekoek and Swarttouw 1998, p. 7).
(Koekoek and Swarttouw 1998, p. 7). 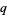 -analogs provided the basis for the Askey-Wilson classification of all orthogonal polynomials.
-analogs provided the basis for the Askey-Wilson classification of all orthogonal polynomials.
A physical motivation for 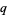 -special functions is provided by generalizing the canonical commutation relation
-special functions is provided by generalizing the canonical commutation relation
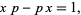 |
(2) |
where  is a generalized coordinate and
is a generalized coordinate and 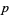 the corresponding generalized momentum, to
the corresponding generalized momentum, to
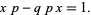 |
(3) |
For example, this immediately leads to the 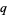 -analog of the Hermite polynomial.
-analog of the Hermite polynomial. 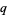 -analogs preserve (or change only slightly) the form of the governing functional equations, and therefore arise in many physical applications, such as exact models in statistical mechanics, noncommutative geometry, and many-particle systems.
-analogs preserve (or change only slightly) the form of the governing functional equations, and therefore arise in many physical applications, such as exact models in statistical mechanics, noncommutative geometry, and many-particle systems.
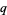 -analogs also have a combinatorial interpretation based on the fact that one can count the elements of some set
-analogs also have a combinatorial interpretation based on the fact that one can count the elements of some set 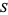 to get the number
to get the number 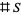 . A so-called "statistic"
. A so-called "statistic" 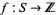 can then be defined which is an integer-valued function on
can then be defined which is an integer-valued function on 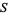 and separates the elements of
and separates the elements of 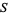 into classes based on what value
into classes based on what value 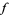 takes on the elements. This relationship can be summarized by writing a polynomial in a new variable, usually taken as
takes on the elements. This relationship can be summarized by writing a polynomial in a new variable, usually taken as 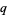 , where the coefficient of
, where the coefficient of 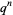 is
is 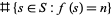 . Evaluating the polynomial at
. Evaluating the polynomial at 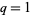 then adds the coefficients together, returning the original
then adds the coefficients together, returning the original 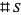 .
.
The 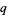 -analog of a mathematical object is generally called the "
-analog of a mathematical object is generally called the "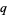 -object," hence q-binomial coefficient, q-factorial, etc. There are generally several
-object," hence q-binomial coefficient, q-factorial, etc. There are generally several 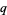 -analogs if there is one, and there is sometimes even a multibasic analog with independent
-analogs if there is one, and there is sometimes even a multibasic analog with independent 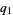 ,
, 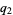 , .... Other types of analogs are also defined, for example the d-analog.
, .... Other types of analogs are also defined, for example the d-analog.
REFERENCES:
Andrews, G. E.; Askey, R.; and Roy, R. Special Functions. Cambridge, England: Cambridge University Press, 1999.
Exton, H. q-Hypergeometric Functions and Applications. New York: Halstead Press, 1983.
Koekoek, R. and Swarttouw, R. F. The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its 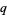 -Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, p. 7, 1998.
-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, p. 7, 1998.
Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, p. 26, 1998.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
بمناسبة مرور 40 يومًا على رحيله الهيأة العليا لإحياء التراث تعقد ندوة ثقافية لاستذكار العلامة المحقق السيد محمد رضا الجلالي
|
|
|