


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-3-2019
Date: 25-5-2019
Date: 18-8-2019
|
The 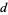 -analog of a complex number
-analog of a complex number 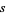 is defined as
is defined as
![[s]_d=1-(2^d)/(s^d)](http://mathworld.wolfram.com/images/equations/d-Analog/NumberedEquation1.gif) |
(1) |
(Flajolet et al. 1995). For integer 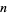 ,
, ![[2]!=1](http://mathworld.wolfram.com/images/equations/d-Analog/Inline4.gif) and
and
![[n]_d!](http://mathworld.wolfram.com/images/equations/d-Analog/Inline5.gif) |
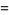 |
![[3][4]...[n]](http://mathworld.wolfram.com/images/equations/d-Analog/Inline7.gif) |
(2) |
 |
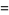 |
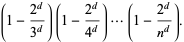 |
(3) |
It can then be extended to complex values via
![[s]_d!=product_(j=1)^infty([j+2])/([j+s])](http://mathworld.wolfram.com/images/equations/d-Analog/NumberedEquation2.gif) |
(4) |
(Flajolet et al. 1995). It satisfies the basic functional identity
![[s]_d!=[s]_d[s-1]_d!.](http://mathworld.wolfram.com/images/equations/d-Analog/NumberedEquation3.gif) |
(5) |
The 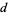 -analog of the polygamma function is
-analog of the polygamma function is
![[psi]_d(s+1)](http://mathworld.wolfram.com/images/equations/d-Analog/Inline12.gif) |
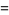 |
![d/(ds)ln[s]_d!](http://mathworld.wolfram.com/images/equations/d-Analog/Inline14.gif) |
(6) |
 |
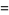 |
![-d·2^dsum_(m=1)^(infty)1/((m+s)[(m+s)^d-2^d]).](http://mathworld.wolfram.com/images/equations/d-Analog/Inline17.gif) |
(7) |
The first few values are
![[psi]_1(s)](http://mathworld.wolfram.com/images/equations/d-Analog/Inline18.gif) |
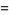 |
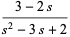 |
(8) |
![[psi]_2(s)](http://mathworld.wolfram.com/images/equations/d-Analog/Inline21.gif) |
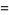 |
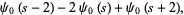 |
(9) |
where 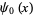 is the digamma function.
is the digamma function.
The 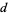 -analog of the Euler-Mascheroni constant
-analog of the Euler-Mascheroni constant 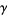 is
is
![[gamma]_d](http://mathworld.wolfram.com/images/equations/d-Analog/Inline27.gif) |
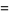 |
![-[psi]_d(3)](http://mathworld.wolfram.com/images/equations/d-Analog/Inline29.gif) |
(10) |
 |
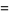 |
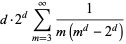 |
(11) |
(Flajolet et al. 1995). The first few values are
![[gamma]_1](http://mathworld.wolfram.com/images/equations/d-Analog/Inline33.gif) |
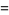 |
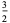 |
(12) |
![[gamma]_2](http://mathworld.wolfram.com/images/equations/d-Analog/Inline36.gif) |
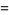 |
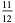 |
(13) |
![[gamma]_3](http://mathworld.wolfram.com/images/equations/d-Analog/Inline39.gif) |
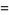 |
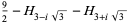 |
(14) |
![[gamma]_4](http://mathworld.wolfram.com/images/equations/d-Analog/Inline42.gif) |
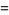 |
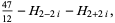 |
(15) |
where 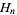 is a harmonic number.
is a harmonic number.
The 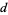 -analog of the harmonic numbers is
-analog of the harmonic numbers is ![[H_2]_d=0](http://mathworld.wolfram.com/images/equations/d-Analog/Inline47.gif) and
and
![[H_n]_d](http://mathworld.wolfram.com/images/equations/d-Analog/Inline48.gif) |
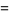 |
![d·2^d(1/(3^(d+1)[3])+1/(4^(d+1)[4])+...+1/(n^(d+1)[n]))](http://mathworld.wolfram.com/images/equations/d-Analog/Inline50.gif) |
(16) |
 |
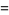 |
![[psi]_d(n+1)+[gamma]_d](http://mathworld.wolfram.com/images/equations/d-Analog/Inline53.gif) |
(17) |
(Flajolet et al. 1995).
The 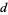 -analog of infinity factorial is given by
-analog of infinity factorial is given by
![[infty]_d!=product_(n=3)^infty(1-(2^d)/(n^d)).](http://mathworld.wolfram.com/images/equations/d-Analog/NumberedEquation4.gif) |
(18) |
This infinite product can be evaluated in closed form in terms of 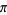 , the hyperbolic sine
, the hyperbolic sine 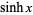 , and gamma functions
, and gamma functions 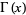 involving roots of unity
involving roots of unity 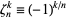 ,
,
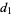 |
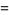 |
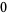 |
(19) |
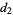 |
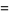 |
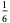 |
(20) |
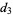 |
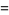 |
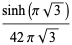 |
(21) |
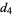 |
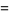 |
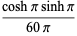 |
(22) |
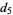 |
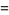 |
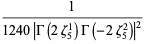 |
(23) |
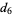 |
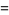 |
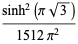 |
(24) |
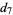 |
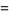 |
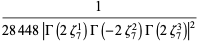 |
(25) |
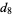 |
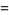 |
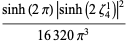 |
(26) |
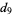 |
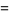 |
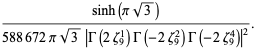 |
(27) |
These are all special cases of a general result for infinite products.
REFERENCES:
Flajolet, P.; Labelle, G.; Laforest, L.; and Salvy, B. "Hypergeometrics and the Cost Structure of Quadtrees." Random Structure Alg. 7, 117-144, 1995. http://algo.inria.fr/flajolet/Publications/publist.html.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|