

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Polylogarithm
المؤلف:
Bailey, D. H.; Borwein, P. B.; and Plouffe, S.
المصدر:
"On the Rapid Computation of Various Polylogarithmic Constants." Math. Comput. 66
الجزء والصفحة:
...
13-8-2019
4243
Polylogarithm
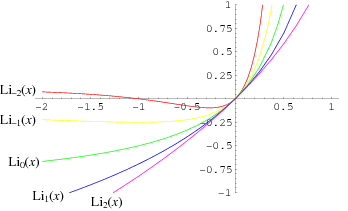
The polylogarithm 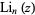 , also known as the Jonquière's function, is the function
, also known as the Jonquière's function, is the function
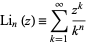 |
(1) |
defined in the complex plane over the open unit disk. Its definition on the whole complex plane then follows uniquely via analytic continuation.
Note that the similar notation 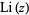 is used for the logarithmic integral.
is used for the logarithmic integral.
The polylogarithm is also denoted 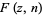 and equal to
and equal to
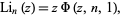 |
(2) |
where 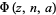 is the Lerch transcendent (Erdélyi et al. 1981, p. 30). The polylogarithm arises in Feynman diagram integrals (and, in particular, in the computation of quantum electrodynamics corrections to the electrons gyromagnetic ratio), and the special cases
is the Lerch transcendent (Erdélyi et al. 1981, p. 30). The polylogarithm arises in Feynman diagram integrals (and, in particular, in the computation of quantum electrodynamics corrections to the electrons gyromagnetic ratio), and the special cases 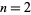 and
and 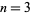 are called the dilogarithm and trilogarithm, respectively. The polylogarithm is implemented in the Wolfram Language as PolyLog[n, z].
are called the dilogarithm and trilogarithm, respectively. The polylogarithm is implemented in the Wolfram Language as PolyLog[n, z].
The polylogarithm also arises in the closed form of the integrals of the Fermi-Dirac distribution
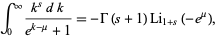 |
(3) |
where 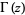 is the gamma function, and the Bose-Einstein distribution
is the gamma function, and the Bose-Einstein distribution
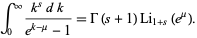 |
(4) |
The special case 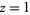 reduces to
reduces to
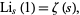 |
(5) |
where 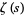 is the Riemann zeta function. Note, however, that the meaning of
is the Riemann zeta function. Note, however, that the meaning of 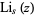 for fixed complex
for fixed complex 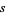 is not completely well-defined, since it depends on how
is not completely well-defined, since it depends on how 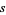 is approached in four-dimensional
is approached in four-dimensional 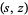 -space.
-space.
The polylogarithm of negative integer order arises in sums of the form
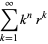 |
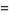 |
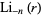 |
(6) |
 |
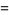 |
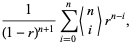 |
(7) |
where 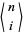 is an Eulerian number. Polylogarithms also arise in sum of generalized harmonic numbers
is an Eulerian number. Polylogarithms also arise in sum of generalized harmonic numbers 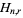 as
as
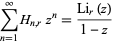 |
(8) |
for 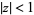 .
.
Special forms of low-order polylogarithms include
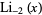 |
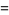 |
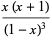 |
(9) |
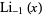 |
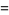 |
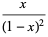 |
(10) |
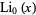 |
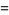 |
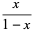 |
(11) |
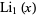 |
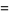 |
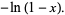 |
(12) |
At arguments 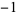 and 1, the general polylogarithms become
and 1, the general polylogarithms become
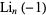 |
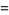 |
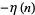 |
(13) |
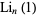 |
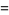 |
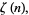 |
(14) |
where 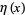 is the Dirichlet eta function and
is the Dirichlet eta function and 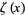 is the Riemann zeta function. The polylogarithm for argument
is the Riemann zeta function. The polylogarithm for argument 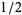 can also be evaluated analytically for small
can also be evaluated analytically for small 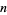 ,
,
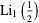 |
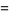 |
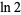 |
(15) |
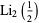 |
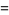 |
![1/(12)[pi^2-6(ln2)^2]](http://mathworld.wolfram.com/images/equations/Polylogarithm/Inline51.gif) |
(16) |
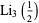 |
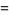 |
![1/(24)[4(ln2)^3-2pi^2ln2+21zeta(3)].](http://mathworld.wolfram.com/images/equations/Polylogarithm/Inline54.gif) |
(17) |
No similar formulas of this type are known for higher orders (Lewin 1991, p. 2). 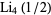 appears in the third-order correction term in the gyromagnetic ratio of the electron.
appears in the third-order correction term in the gyromagnetic ratio of the electron.
The derivative of a polylogarithm is itself a polylogarithm,
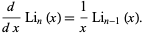 |
(18) |
Bailey et al. showed that
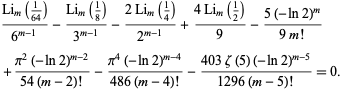 |
(19) |
A number of remarkable identities exist for polylogarithms, including the amazing identity satisfied by 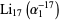 , where
, where 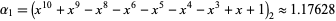 (OEIS A073011) is the smallest Salem constant, i.e., the largest positive root of the polynomial in Lehmer's Mahler measure problem (Cohen et al. 1992; Bailey and Broadhurst 1999; Borwein and Bailey 2003, pp. 8-9).
(OEIS A073011) is the smallest Salem constant, i.e., the largest positive root of the polynomial in Lehmer's Mahler measure problem (Cohen et al. 1992; Bailey and Broadhurst 1999; Borwein and Bailey 2003, pp. 8-9).
No general algorithm is known for integration of polylogarithms of functions.
REFERENCES:
Bailey, D. H.; Borwein, P. B.; and Plouffe, S. "On the Rapid Computation of Various Polylogarithmic Constants." Math. Comput. 66, 903-913, 1997.
Bailey, D. H. and Broadhurst, D. J. "A Seventeenth-Order Polylogarithm Ladder." 20 Jun 1999. http://arxiv.org/abs/math.CA/9906134.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Borwein, J. M.; Bradley, D. M.; Broadhurst, D. J.; and Lisonek, P. "Special Values of Multidimensional Polylogarithms." Trans. Amer. Math. Soc. 353, 907-941, 2001.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 323-326, 1994.
Cohen, H.; Lewin, L.; and Zagier, D. "A Sixteenth-Order Polylogarithm Ladder." Exper. Math. 1, 25-34, 1992. http://www.expmath.org/expmath/volumes/1/1.html.
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Higher Transcendental Functions, Vol. 1. New York: Krieger, pp. 30-31, 1981.
Jonquière, A. "Ueber eine Klasse von Transcendenten, welche durch mehrmahlige Integration rationaler Funktionen enstehen." Öfversigt af Kongl. Vetenskaps-Akademiens Förhandlingar 45, 522-531, 1888.
Jonquière, A. "Note sur la série 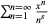 ." Öfversigt af Kongl. Vetenskaps-Akademiens Förhandlingar 46, 257-268, 1888.
." Öfversigt af Kongl. Vetenskaps-Akademiens Förhandlingar 46, 257-268, 1888.
Jonquière, A. "Ueber einige Transcendente, welche bei den wiederholten Integration rationaler Funktionen auftreten." Bihang till Kongl. Svenska Vetenskaps-Akademiens Handlingar 15, 1-50, 1889.
Jonquière, A. "Note sur la série 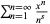 ." Bull. Soc. Math. France 17, 142-152, 1889.
." Bull. Soc. Math. France 17, 142-152, 1889.
Lewin, L. Dilogarithms and Associated Functions. London: Macdonald, 1958.
Lewin, L. Polylogarithms and Associated Functions. New York: North-Holland, 1981.
Lewin, L. (Ed.). Structural Properties of Polylogarithms. Providence, RI: Amer. Math. Soc., 1991.
Nielsen, N. Der Euler'sche Dilogarithms. Leipzig, Germany: Halle, 1909.
Prudnikov, A. P.; Marichev, O. I.; and Brychkov, Yu. A. "The Generalized Zeta Function 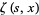 , Bernoulli Polynomials
, Bernoulli Polynomials 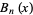 , Euler Polynomials
, Euler Polynomials 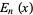 , and Polylogarithms
, and Polylogarithms 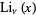 ." §1.2 in Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, pp. 23-24, 1990.
." §1.2 in Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, pp. 23-24, 1990.
Sloane, N. J. A. Sequence A073011 in "The On-Line Encyclopedia of Integer Sequences."
Truesdell, C. "On a Function Which Occurs in the Theory of the Structure of Polymers." Ann. Math. 46, 114-157, 1945.
Zagier, D. "Special Values and Functional Equations of Polylogarithms." Appendix A in Structural Properties of Polylogarithms (Ed. L. Lewin). Providence, RI: Amer. Math. Soc., 1991.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















