
Multivariate Zeta Function
 المؤلف:
Akiyama, S.; Egami, S.; and Tanigawa, Y.
المؤلف:
Akiyama, S.; Egami, S.; and Tanigawa, Y.
 المصدر:
"Analytic Continuation of Multiple Zeta-Functions and Their Values at Non-Positive Integers." Acta Arith. 98
المصدر:
"Analytic Continuation of Multiple Zeta-Functions and Their Values at Non-Positive Integers." Acta Arith. 98
 الجزء والصفحة:
...
الجزء والصفحة:
...
 28-7-2019
28-7-2019
 2967
2967
Multivariate Zeta Function
Multivariate zeta function, also called multiple zeta values, multivariate zeta constants (Bailey et al. 2006, p. 43), multi-zeta values (Bailey et al. 2006, p. 17), and multivariate zeta values, are defined by
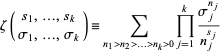 |
(1)
|
(Broadhurst 1996, 1998). This can be written in the more compact and convenient form
![zeta(a_1,...,a_k)=sum_(n_1>n_2>...>n_k>0)product_(j=1)^k([sgn(a_j)]^(n_j))/(n_j^(|a_j|))
=sum_(n_1>n_2>...>n_k>0)([sgn(a_1)]^(n_1)[sgn(a_2)]^(n_2)...[sgn(a_k)]^(n_k))/(n_1^(|a_1|)n_2^(|a_2|)...|n_k|^(|a_k|)).](http://mathworld.wolfram.com/images/equations/MultivariateZetaFunction/NumberedEquation2.gif) |
(2)
|
(Broadhurst 1996; Bailey et al. 2007, p. 38).
The notation 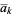 (as opposed to
(as opposed to 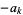 ) is sometimes also used to indicate that a factor of 1 in the numerator is replaced by a corresponding factor of
) is sometimes also used to indicate that a factor of 1 in the numerator is replaced by a corresponding factor of 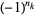 . In addition, the notation
. In addition, the notation 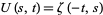 is used in quantum field theory.
is used in quantum field theory.
In particular, for 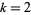 , these correspond to the usual Euler sums
, these correspond to the usual Euler sums
(Broadhurst 1996).
Multivariate zeta functions (and their derivatives) also arise in the closed-form evaluation of definite integrals involving the log cosine function (Oloa 2011).
These sums satisfy
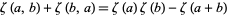 |
(7)
|
for 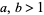 , as well as
, as well as
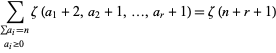 |
(8)
|
for nonnegative integers 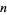 and
and 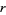 (Bailey et al. 2007). These give the special cases
(Bailey et al. 2007). These give the special cases
(Bailey et al. 2007).
A different kind of special case is given by
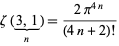 |
(12)
|
(Borwein and Bailey 2003, p. 26; Borwein et al. 2004, Ch. 2, Ex. 29).
Other special values include
(Bailey et al. 2007, pp. 223 and 251). Closed forms are known for all 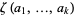 with
with 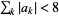 are known (Bailey et al. 2006, p. 39).
are known (Bailey et al. 2006, p. 39).
Amazingly,
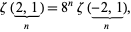 |
(20)
|
found by J. Borwein and D. Broadhurst in 1996 (Bailey et al. 2006, p. 17).
REFERENCES:
Akiyama, S.; Egami, S.; and Tanigawa, Y. "Analytic Continuation of Multiple Zeta-Functions and Their Values at Non-Positive Integers." Acta Arith. 98, 107-116, 2001.
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. "Computation of Multivariate Zeta Constants." §2.5 in Experimental Mathematics in Action. Wellesley, MA: A K Peters, pp. 43 and 223-224, 2007.
Bailey, D. H.; Borwein, J. M.; Kapoor, V.; and Weisstein, E. W. "Ten Problems in Experimental Mathematics." Amer. Math. Monthly 113, 481-509, 2006.
Borwein, J. and Bailey, D. "Quantum Field Theory." §2.6 in Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, pp. 58-59, 2003.
Borwein, J.; Bailey, D.; and Girgensohn, R. Ch. 3 in Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.
Borwein, J. M.; Bradley, D. M.; Broadhurst, D. J.; and Lisonek, P. "Special Values of Multidimensional Polylogarithms." Trans. Amer. Math. Soc. 353, 907-941, 2001.
Broadhurst, D. J. "On the Enumeration of Irreducible 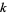 -Fold Euler Sums and Their Roles in Knot Theory and Field Theory." April 22, 1996. http://arxiv.org/abs/hep-th/9604128
-Fold Euler Sums and Their Roles in Knot Theory and Field Theory." April 22, 1996. http://arxiv.org/abs/hep-th/9604128
Broadhurst, D. J. "Massive 3-Loop Feynman Diagrams Reducible to 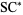 Primitives of Algebras of the Sixth Root of Unity." March 11, 1998. http://arxiv.org/abs/hep-th/9803091.
Primitives of Algebras of the Sixth Root of Unity." March 11, 1998. http://arxiv.org/abs/hep-th/9803091.
Oloa, O. "A Log-Cosine Integral Involving a Derivative of a MZV." Preprint. Apr. 18, 2011.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


