


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-1-2016
Date: 30-12-2015
Date: 10-1-2016
|
Factors and Multiples
Factors are parts of numbers that, multiplied together, give a larger number. Every number has at least two factors, one and the number itself. On the other hand, multiples are numbers where the same number is repeated, as if you were counting by that number. For example, the multiples of 2 start with 2 and are: 2, 4, 6, 8, 10 . . . and so on. Each additional number is a multiple of 2.
Factors and multiples are especially important in working with expanding and reducing fractions, as well as finding patterns in numbers. Finding the greatest common factor, least common multiple, and prime factors of a number are important skills you will learn in this section.
A factor is a part of a number and two factors multiplied together produce a product. Every number has at least two factors, possibly more. For example, the number 2 has two factors, 1 and 2, because 2 x 1 = 2. Some numbers have more than two factors, like 10. Factors of 10 would include, of course, 1 and 10, but they would also include 2 and 5, because 2 x 5 = 10. Therefore, if we were asked to list factors of 10, we would write: 1, 2, 5, 10.
Let’s practice this. List the factor pairs and factor lists of the following numbers: 15, 20, 17, 43, 28, 32, 99
Solutions—first we’ll list the factor pairs, and then we’ll list the factor list from smallest to largest:
15: 1 x 15, 3 x 5. Answer: 1, 3, 5, 15.
20: 1 x 20, 2 x 10, 4 x 5. Answer: 1, 2, 4, 5, 10, 20.
17: 1 x 17. Answer: 1, 17.
43: 1 x 43. Answer: 1, 43.
28: 1 x 28, 2 x 14, 4 x 7. Answer: 1, 2, 4, 7, 14, 28.
32: 1 x 32, 2 x 16, 4 x 8. Answer: 1, 2, 4, 8, 16, 32.
99: 1 x 99, 3 x 33, 9 x 11. Answer: 1, 3, 9, 11, 33, 99.
Notice that when we wrote our lists, we started by writing the number given to us originally, followed by a colon ( : ). This is standard notation, but not absolutely necessary. Next, we wrote factor pairs. Factor pairs are always the multiplication problems, and look like this: 2 x 1, but do not contain the = or the answer. Last, we listed the factors themselves, separated by commas. You may be asked for just the factor pairs, or just the factor list, or both. Make sure you give the answer that fully completes the question you’re asked.
After you learn how to find factors, you may be asked to find the greatest common factor (GCF) between two numbers. The GCF is the largest factor that both numbers share. This means that you would list all the factors for each number. Then, you would circle (or underline, etc) all the factors that the numbers have in common. After that, you would report the greatest number (out of the common—circled—numbers).
For example, find the greatest common factor of 24 and 32. First, list the factors for each number, like this:
24: 1, 2, 3, 4, 6, 8, 12, 24.
32: 1, 2, 4, 8, 16, 32.
Now, go through and circle or underline (we’re going to underline) the common multiples, like this:
24: 1, 2, 3, 4, 6, 8, 12, 24.
32: 1, 2, 4, 8, 16, 32.
Now, look only at the underlined numbers. Which number is the biggest? We can see that the greatest number we have on our common factors list is 8, so 8 is our greatest common factor.
Greatest common factors are most often used when reducing fractions. It would be applied like this:
Reduce 15/20.
First, you would list the factors of both 15 and 20, like this:
15: 1, 3, 5, 15.
20: 1, 2, 4, 5, 10, 20.
Now, you would underline the common factors between the two numbers, like this:
15: 1, 3, 5, 15.
20: 1, 2, 4, 5, 10, 20.
Now, look at the common factors, and find the greatest of the underlined numbers. You will see that 5 is the greatest common factor. This tells you that you can reduce the fraction by 5, like this:

Thus, your reduced fraction is 3/4. Notice that the problem did not directly ask you to find the GCF, but finding it helped you reduce the fraction into lowest terms.
A multiple is a product of a number and an integer, or more simply, when you multiply two whole numbers together. Every number has an infinite number of multiples. For example, the multiples of 2 are 2, 4, 6, 8, 10, 12, 14 and so on, to infinity. You may be asked to make a list of multiples until you hit a certain number (for example, list the multiples of 2 from 2 to 50) or you might be asked to list a certain number of multiples (for example, list the first 5 multiples of 4). The important part here is that you carefully read the directions and make sure that you understand what the question is asking of you before you answer. Here are several examples:
List the first five multiples of the following numbers: 3, 6, 9, 10, 7, 12, 50
3: 3, 6, 9, 12, 15
6: 6, 12, 18, 24, 30
9: 9, 18, 27, 36, 45
10: 10, 20, 30, 40, 50
7: 7, 14, 21, 28, 35
12: 12, 24, 36, 48, 60
50: 50, 100, 150, 200, 250
You also might recognize multiples as "counting by" the above listed numbers.
Once you learn what multiples are and how to find them, you will often be asked to find the "least common multiple" between two numbers. For example, this is how you find the least common multiple (LCM) between 4 and 5:
First, list the multiples of each number. Now, this could go on until infinity, so we recommend only listing the first 5 multiples of each number, and then continuing on if you need to.
4: 4, 8, 12, 16, 20
5: 5, 10, 15, 20, 25
Next, underline (or circle) any factors they have in common. If they don’t have common factors, you need to keep going (check the next five multiples). If they do have common multiples, underline them, like this:
4: 4, 8, 12, 16, 20
5: 5, 10, 15, 20, 25
Now, you have to find the least common multiple. In our example, we only have one common multiple, so that is our LCM. However, if we had more than one common multiple, we would pick the smallest one. Therefore, our LCM between 4 and 5 is 20.
Very rarely will you be asked to simply find the LCM between two numbers. However, this process is particularly useful in finding common denominators. For example, let’s say we had the problem 5/8 + 2/5. We would first need to find a common denominator. Here’s how we would use LCMs to find the common denominator.
First, we need to list the multiples of each of the denominators in the problem, 8 and 5.
8: 8, 16, 24, 32, 40
5: 5, 10, 15, 20, 25
At this point, we don’t see any common multiples, so we’ll list 5 more for each one:
8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80
5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50
Now, we underline the common multiples, like this:
8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80
5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50
We notice that 40 is our only common multiple, thus for this problem it is our LCM as well. Next, you would use the LCM as your new common denominator between the two fractions. You would expand each fraction so that it has a denominator of 40, like this:

Then, you would just add the two fractions together: 25/40 + 16/40 = 41/40. Then, you would convert your fraction into a mixed number (since the fraction is improper) and you would end up with 1 1/40.
Prime factorization is used to find prime factors of any given number. Prime numbers are numbers that only have factors of 1 and the number (like 3—the only factors of 3 are 1 and 3). Prime factorization allows you to easily find all the prime factors of a number, and all numbers have a prime factorization. There are several different ways to write prime factorization; we’re going to show you the “pine tree” method. No matter which way you write it, you’ll be getting the same numbers for your factorization.
In order to find the prime factors, you’re first going to look at the number you have and think of two numbers that multiply together to produce that number. Let’s look at the number 45. Can you think of two numbers that multiply together to get 45? Well, we know that 9 x 5 is 45. Now, we look at 9 and 5. Are either of these prime numbers? We know that 5 is a prime number because the only numbers that multiply to give us 5 are 1 x 5. We leave the 5 alone, and look at the 9. Is 9 a prime number? No, it’s not, so we need to think of what multiplies to give us 9. We know that 3 x 3 is 9, so 9 turns into 3 x 3. Now, we look at each 3. Is 3 a prime number? We know that both 3s are prime numbers, because the only thing that multiplies to give us 3 is 1 x 3. Thus, our prime factorization is 3 x 3 x 5.
We often use a specific way of writing this, as we mentioned earlier, called the “pine tree” format. Prime factorization does not have to be written this way, but it is easier to organize your problem. The “pine tree” format looks like this:

It may not look too much like a pine tree with a short factorization like 45 has. However, some numbers stretch out even more, and the shape looks similar to a pine tree. Each level of branches is a separate multiplication problem that includes the factors of the number. Remember, this is merely one way of writing the factorization. The main goal is for you to be left with the prime factors of whatever number you’re working with. Let’s look at one more example:
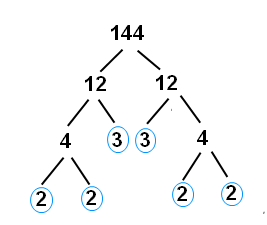
Each level of branches is another multiplication problem resulting in the previous number. From the top down, you have 144, which you can split into 12 x 12. Then, each twelve can be split into 3 x 4. Each 4 can be split into 2 x 2. Thus, the prime factorization (the numbers circled in blue in the diagram) is 2 x 2 x 2 x 2 x 3 x 3. Typically, we list the prime numbers in order from least to greatest. Since they’re being multiplied, you don’t have to keep them in factor pairs to order them.



|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
|
|
|