


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-6-2019
Date: 19-5-2019
Date: 12-10-2018
|
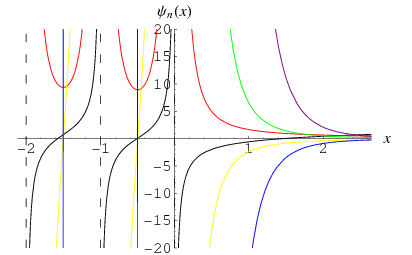
A special function mostly commonly denoted 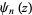 ,
, 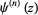 , or
, or 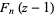 which is given by the
which is given by the 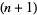 st derivative of the logarithm of the gamma function
st derivative of the logarithm of the gamma function 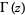 (or, depending on the definition, of the factorial
(or, depending on the definition, of the factorial 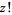 ). This is equivalent to the
). This is equivalent to the 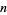 th normal derivative of the logarithmic derivative of
th normal derivative of the logarithmic derivative of 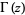 (or
(or 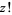 ) and, in the former case, to the
) and, in the former case, to the 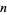 th normal derivative of the digamma function
th normal derivative of the digamma function 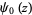 . Because of this ambiguity in definition, two different notations are sometimes (but not always) used, namely
. Because of this ambiguity in definition, two different notations are sometimes (but not always) used, namely
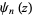 |
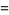 |
![(d^(n+1))/(dz^(n+1))ln[Gamma(z)]](http://mathworld.wolfram.com/images/equations/PolygammaFunction/Inline14.gif) |
(1) |
 |
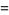 |
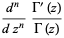 |
(2) |
 |
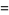 |
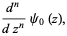 |
(3) |
which, for 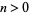 can be written as
can be written as
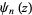 |
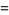 |
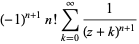 |
(4) |
 |
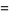 |
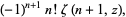 |
(5) |
where 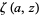 is the Hurwitz zeta function.
is the Hurwitz zeta function.
The alternate notation
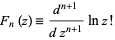 |
(6) |
is sometimes used, with the two notations connected by
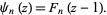 |
(7) |
Unfortunately, Morse and Feshbach (1953) adopt a notation no longer in standard use in which Morse and Feshbach's "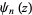 " is equal to
" is equal to 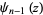 in the usual notation. Also note that the function
in the usual notation. Also note that the function 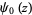 is equivalent to the digamma function
is equivalent to the digamma function 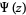 and
and 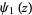 is sometimes known as the trigamma function.
is sometimes known as the trigamma function.
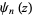 is implemented in the Wolfram Language as PolyGamma[n, z] for positive integer
is implemented in the Wolfram Language as PolyGamma[n, z] for positive integer 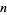 . In fact, PolyGamma[nu, z] is supported for all complex
. In fact, PolyGamma[nu, z] is supported for all complex  (Grossman 1976; Espinosa and Moll 2004).
(Grossman 1976; Espinosa and Moll 2004).
The polygamma function obeys the recurrence relation
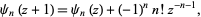 |
(8) |
the reflection formula
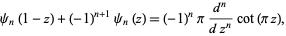 |
(9) |
and the multiplication formula,
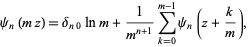 |
(10) |
where 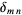 is the Kronecker delta.
is the Kronecker delta.
The polygamma function is related to the Riemann zeta function 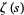 and the generalized harmonic numbers
and the generalized harmonic numbers 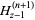 by
by
![psi_n(z)=(-1)^(n+1)n![zeta(n+1)-H_(z-1)^((n+1))]](http://mathworld.wolfram.com/images/equations/PolygammaFunction/NumberedEquation6.gif) |
(11) |
for 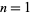 , 2, ..., and in terms of the Hurwitz zeta function
, 2, ..., and in terms of the Hurwitz zeta function 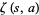 as
as
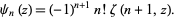 |
(12) |
The Euler-Mascheroni constant is a special value of the digamma function 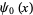 , with
, with
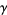 |
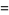 |
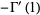 |
(13) |
 |
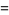 |
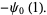 |
(14) |
In general, special values for integral indices are given by
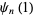 |
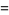 |
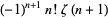 |
(15) |
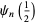 |
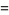 |
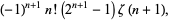 |
(16) |
giving the digamma function, trigamma function, and tetragamma function identities
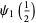 |
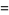 |
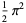 |
(17) |
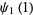 |
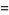 |
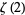 |
(18) |
 |
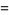 |
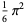 |
(19) |
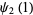 |
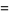 |
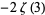 |
(20) |
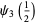 |
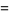 |
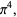 |
(21) |
and so on.
The polygamma function can be expressed in terms of Clausen functions for rational arguments and integer indices. Special cases are given by
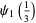 |
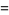 |
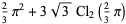 |
(22) |
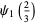 |
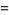 |
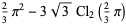 |
(23) |
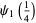 |
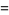 |
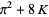 |
(24) |
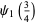 |
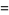 |
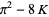 |
(25) |
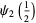 |
 |
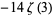 |
(26) |
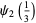 |
 |
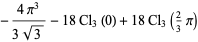 |
(27) |
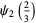 |
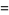 |
 |
(28) |
 |
 |
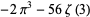 |
(29) |
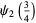 |
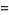 |
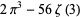 |
(30) |
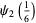 |
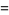 |
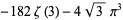 |
(31) |
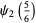 |
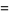 |
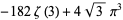 |
(32) |
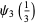 |
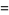 |
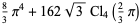 |
(33) |
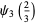 |
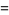 |
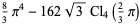 |
(34) |
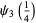 |
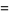 |
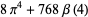 |
(35) |
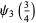 |
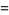 |
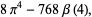 |
(36) |
where 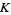 is Catalan's constant,
is Catalan's constant, 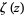 is the Riemann zeta function, and
is the Riemann zeta function, and 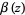 is the Dirichlet beta function.
is the Dirichlet beta function.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Polygamma Functions." §6.4 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 260, 1972.
Adamchik, V. S. "Polygamma Functions of Negative Order." J. Comput. Appl. Math. 100, 191-199, 1999.
Arfken, G. "Digamma and Polygamma Functions." §10.2 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 549-555, 1985.
Berndt, B. C. Ramanujan's Notebooks: Part I. New York: Springer-Verlag, p. 163, 1985.
Davis, H. T. Tables of the Higher Mathematical Functions. Bloomington, IN: Principia Press, 1933.
Espinosa, O. and Moll, V. H. "A Generalized Polygamma Function." Integral Trans. Special Func. 15, 101-115, 2004.
Grossman, N. "Polygamma Functions of Arbitrary Order." SIAM J. Math. Anal. 7, 366-372, 1976.
Hansen, E. R. A Table of Series and Products. Englewood Cliffs, NJ: Prentice-Hall, 1975.
Kölbig, K. S. "The Polygamma Function 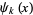 for
for 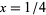 and
and 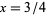 ." J. Comp. Appl. Math. 75, 43-46, 1996.
." J. Comp. Appl. Math. 75, 43-46, 1996.
Kölbig, K. S. "The Polygamma Function and the Derivatives of the Cotangent Function for Rational Arguments." Report CN/96/5. CERN Computing and Networks Division, 1996.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 422-424, 1953.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|