

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Subfactorial
المؤلف:
Cajori, F.
المصدر:
A History of Mathematical Notations, Vol. 2. New York: Cosimo Classics, 2007.
الجزء والصفحة:
...
19-5-2019
4117
Subfactorial
The 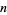 th subfactorial (also called the derangement number; Goulden and Jackson 1983, p. 48; Graham et al. 2003, p. 1050) is the number of permutations of
th subfactorial (also called the derangement number; Goulden and Jackson 1983, p. 48; Graham et al. 2003, p. 1050) is the number of permutations of 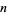 objects in which no object appears in its natural place (i.e., "derangements").
objects in which no object appears in its natural place (i.e., "derangements").
The term "subfactorial "was introduced by Whitworth (1867 or 1878; Cajori 1993, p. 77). Euler (1809) calculated the first ten terms.
The first few values of 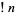 for
for 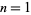 , 2, ... are 0, 1, 2, 9, 44, 265, 1854, 14833, ... (OEIS A000166). For example, the only derangements of
, 2, ... are 0, 1, 2, 9, 44, 265, 1854, 14833, ... (OEIS A000166). For example, the only derangements of {1,2,3}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline5.gif" style="height:14px; width:47px" /> are
{2,3,1}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline6.gif" style="height:14px; width:47px" /> and
{3,1,2}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline7.gif" style="height:14px; width:47px" />, so
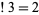 . Similarly, the derangements of
. Similarly, the derangements of {1,2,3,4}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline9.gif" style="height:14px; width:62px" /> are
{2,1,4,3}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline10.gif" style="height:14px; width:62px" />,
{2,3,4,1}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline11.gif" style="height:14px; width:62px" />,
{2,4,1,3}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline12.gif" style="height:14px; width:62px" />,
{3,1,4,2}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline13.gif" style="height:14px; width:62px" />,
{3,4,1,2}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline14.gif" style="height:14px; width:62px" />,
{3,4,2,1}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline15.gif" style="height:14px; width:62px" />,
{4,1,2,3}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline16.gif" style="height:14px; width:62px" />,
{4,3,1,2}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline17.gif" style="height:14px; width:62px" />, and
{4,3,2,1}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline18.gif" style="height:14px; width:62px" />, so
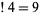 .
.
Sums and formulas for 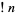 include
include
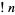 |
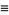 |
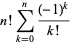 |
(1) |
 |
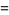 |
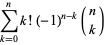 |
(2) |
 |
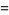 |
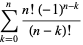 |
(3) |
 |
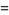 |
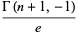 |
(4) |
where 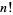 is a factorial,
is a factorial, 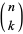 is a binomial coefficient, and
is a binomial coefficient, and 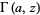 is the incomplete gamma function.
is the incomplete gamma function.
Subfactorials are implemented in the Wolfram Language as Subfactorial[n].
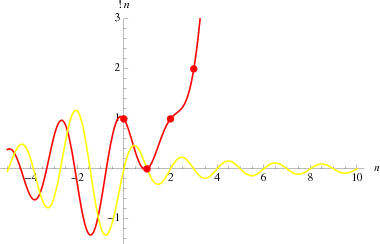
A plot the real and imaginary parts of the subfactorial generalized to any real argument is illustrated above, with the usual integer-valued subfactorial corresponding to nonnegative integer 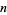 .
.
The subfactorials are also called the rencontres numbers and satisfy the recurrence relations
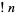 |
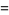 |
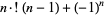 |
(5) |
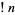 |
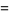 |
![(n-1)[!(n-2)+!(n-1)].](http://mathworld.wolfram.com/images/equations/Subfactorial/Inline42.gif) |
(6) |
The subfactorial can be considered a special case of a restricted rooks problem.
The subfactorial has generating function
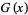 |
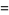 |
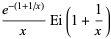 |
(7) |
 |
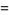 |
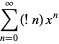 |
(8) |
 |
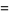 |
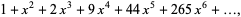 |
(9) |
where 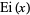 is the exponential integral, and exponential generating function
is the exponential integral, and exponential generating function
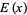 |
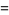 |
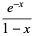 |
(10) |
 |
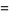 |
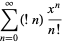 |
(11) |
 |
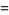 |
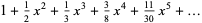 |
(12) |
(OEIS A053557 and A053556).
Subfactorials are commonly denoted 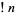 ,
, 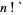 (Graham et al. 2003, p. 194),
(Graham et al. 2003, p. 194), 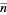 (Dörrie 1965, p. 19),
(Dörrie 1965, p. 19), 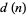 (Pemmaraju and Skiena 2003, p. 106),
(Pemmaraju and Skiena 2003, p. 106), 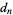 (Goulden and Jackson 1983, p. 48; van Lint and Wilson 1992, p. 90), or
(Goulden and Jackson 1983, p. 48; van Lint and Wilson 1992, p. 90), or 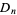 (Riordan 1980, p. 59; Stanley 1997, p. 489), the latter being especially used when viewing them as derangements.
(Riordan 1980, p. 59; Stanley 1997, p. 489), the latter being especially used when viewing them as derangements.
Another equation is given by
![!n=[(n!)/e],](http://mathworld.wolfram.com/images/equations/Subfactorial/NumberedEquation1.gif) |
(13) |
where 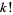 is the usual factorial and
is the usual factorial and ![[x]](http://mathworld.wolfram.com/images/equations/Subfactorial/Inline69.gif) is the nearest integer function. M. Hassani (pers. comm., Oct. 28, 2004) gave the forms
is the nearest integer function. M. Hassani (pers. comm., Oct. 28, 2004) gave the forms
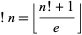 |
(14) |
for 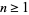 and
and
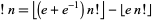 |
(15) |
for 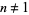 , where
, where 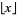 is the floor function.
is the floor function.
An integral for 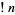 is given by
is given by
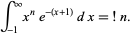 |
(16) |
A continued fraction for 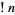 is given by
is given by
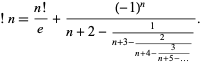 |
(17) |
The numbers of decimal digits in 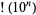 for
for 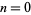 , 1, ... are 7, 158, 2568, 35660, 456574, 5565709, 65657059, ... (OEIS A114485).
, 1, ... are 7, 158, 2568, 35660, 456574, 5565709, 65657059, ... (OEIS A114485).
The only prime subfactorial is 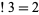 .
.
The only number equal to the sum of subfactorials of its digits is
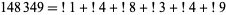 |
(18) |
(Madachy 1979).
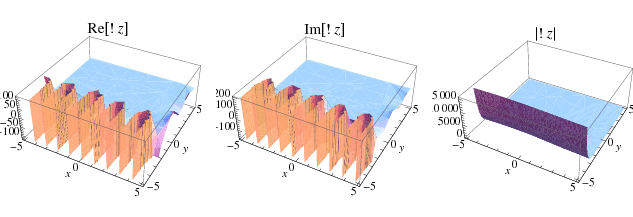
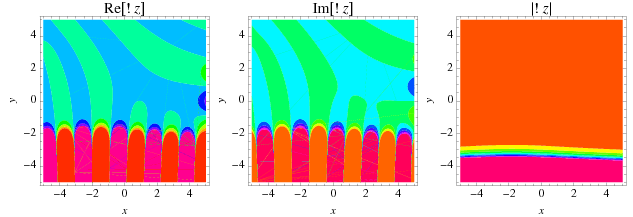
The subfactorial may be analytically continued to the complex plane, as illustrated above.
REFERENCES:
Cajori, F. A History of Mathematical Notations, Vol. 2. New York: Cosimo Classics, 2007.
Dörrie, H. §6 in 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, pp. 19-21, 1965.
Euler, L. "Solution quaestionis curiosae ex doctrina combinationum." Mémoires Académie Sciences St. Pétersbourg 3, 57-64, 1809. Reprinted in Opera Omnia, Series Prima, Vol. 7. Leipzig, Germany: Teubner, pp. 435-440, 1915.
Goulden, I. P. and Jackson, D. M. Combinatorial Enumeration. New York: Wiley, 1983.
Graham, R. L.; Grötschel, M.; and Lovász, L. (Eds.). Handbook of Combinatorics, Vol. 2. Cambridge, MA: MIT Press, 2003.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, p. 167, 1979.
Pemmaraju, S. and Skiena, S. Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica.Cambridge, England: Cambridge University Press, 2003.
Riordan, J. An Introduction to Combinatorial Analysis. New York: Wiley, 1980.
Sloane, N. J. A. Sequences A000166/M1937, A053556, A053557, and A114485 in "The On-Line Encyclopedia of Integer Sequences."
Sloane, N. J. A. and Plouffe, S. Figure M1937 in The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Stanley, R. P. Enumerative Combinatorics, Vol. 1. Cambridge, England: Cambridge University Press, p. 67, 1997.
van Lint, J. H. and Wilson, R. M. A Course in Combinatorics. New York: Cambridge University Press, 1992.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 27, 1986.
Whitworth, W. A. Choice and Chance, Two Chapters of Arithmetic, with an Appendix Containing the Algebraical Treatment of Permutations and Combinations Newly Set Forth. Cambridge, England: Deighton, Bell, 1867.
Whitworth, W. A. Messenger Math. 1878.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















