


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-6-2019
Date: 21-9-2019
Date: 19-9-2018
|
The double factorial of a positive integer 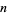 is a generalization of the usual factorial
is a generalization of the usual factorial 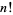 defined by
defined by
 |
(1) |
Note that 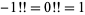 , by definition (Arfken 1985, p. 547).
, by definition (Arfken 1985, p. 547).
The origin of the notation 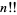 appears not to not be widely known and is not mentioned in Cajori (1993).
appears not to not be widely known and is not mentioned in Cajori (1993).
For 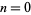 , 1, 2, ..., the first few values are 1, 1, 2, 3, 8, 15, 48, 105, 384, ... (OEIS A006882). The numbers of decimal digits in
, 1, 2, ..., the first few values are 1, 1, 2, 3, 8, 15, 48, 105, 384, ... (OEIS A006882). The numbers of decimal digits in 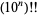 for
for 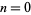 , 1, ... are 1, 4, 80, 1285, 17831, 228289, 2782857, 32828532, ... (OEIS A114488).
, 1, ... are 1, 4, 80, 1285, 17831, 228289, 2782857, 32828532, ... (OEIS A114488).
The double factorial is implemented in the Wolfram Language as n!! or Factorial2[n].
The double factorial is a special case of the multifactorial.
The double factorial can be expressed in terms of the gamma function by
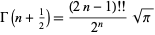 |
(2) |
(Arfken 1985, p. 548).
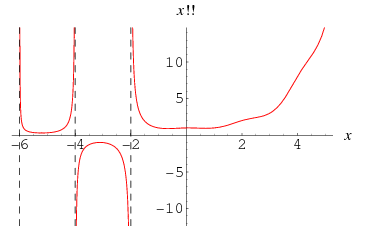
The double factorial can also be extended to negative odd integers using the definition
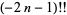 |
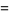 |
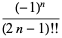 |
(3) |
 |
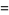 |
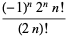 |
(4) |
for 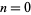 , 1, ... (Arfken 1985, p. 547).
, 1, ... (Arfken 1985, p. 547).
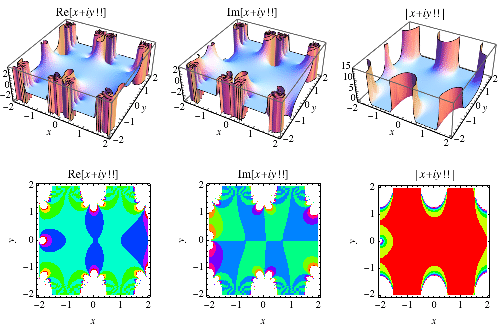 |
Similarly, the double factorial can be extended to complex arguments as
![z!!=2^([1+2z-cos(piz)]/4)pi^([cos(piz)-1]/4)Gamma(1+1/2z).](http://mathworld.wolfram.com/images/equations/DoubleFactorial/NumberedEquation3.gif) |
(5) |
There are many identities relating double factorials to factorials. Since
![(2n+1)!!2^nn!
=[(2n+1)(2n-1)...1][2n][2(n-1)][2(n-2)]...2·1
=[(2n+1)(2n-1)...1][2n(2n-2)(2n-4)...2]
=(2n+1)(2n)(2n-1)(2n-2)(2n-3)(2n-4)...2·1
=(2n+1)!,](http://mathworld.wolfram.com/images/equations/DoubleFactorial/NumberedEquation4.gif) |
(6) |
it follows that 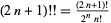 . For
. For 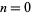 , 1, ..., the first few values are 1, 3, 15, 105, 945, 10395, ... (OEIS A001147).
, 1, ..., the first few values are 1, 3, 15, 105, 945, 10395, ... (OEIS A001147).
Also, since
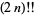 |
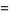 |
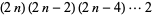 |
(7) |
 |
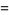 |
![[2(n)][2(n-1)][2(n-2)]...2](http://mathworld.wolfram.com/images/equations/DoubleFactorial/Inline22.gif) |
(8) |
 |
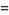 |
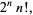 |
(9) |
it follows that 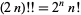 . For
. For 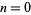 , 1, ..., the first few values are 1, 2, 8, 48, 384, 3840, 46080, ... (OEIS A000165).
, 1, ..., the first few values are 1, 2, 8, 48, 384, 3840, 46080, ... (OEIS A000165).
Finally, since
![(2n-1)!!2^nn!
=[(2n-1)(2n-3)...1][2n][2(n-1)][2(n-2)]...2(1)
=(2n-1)(2n-3)...1][2n(2n-2)(2n-4)...2]
=2n(2n-1)(2n-2)(2n-3)(2n-4)...2(1)
=(2n)!,](http://mathworld.wolfram.com/images/equations/DoubleFactorial/NumberedEquation5.gif) |
(10) |
it follows that
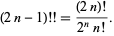 |
(11) |
For 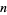 odd,
odd,
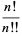 |
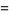 |
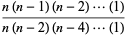 |
(12) |
 |
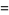 |
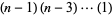 |
(13) |
 |
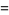 |
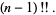 |
(14) |
For 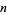 even,
even,
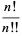 |
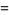 |
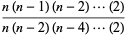 |
(15) |
 |
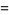 |
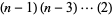 |
(16) |
 |
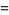 |
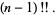 |
(17) |
Therefore, for any 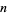 ,
,
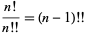 |
(18) |
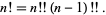 |
(19) |
The double factorial satisfies the beautiful series
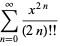 |
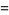 |
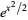 |
(20) |
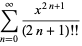 |
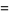 |
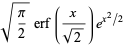 |
(21) |
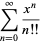 |
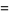 |
![1/2e^(x^2/2)[sqrt(2pi)erf(x/(sqrt(2)))+2].](http://mathworld.wolfram.com/images/equations/DoubleFactorial/Inline57.gif) |
(22) |
The latter gives rhe sum of reciprocal double factorials in closed form as
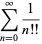 |
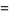 |
![sqrt(e)[1+sqrt(pi/2)erf(1/2sqrt(2))]](http://mathworld.wolfram.com/images/equations/DoubleFactorial/Inline60.gif) |
(23) |
 |
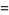 |
![sqrt(e)[1/2sqrt(2)+gamma(1/2,1/2)]](http://mathworld.wolfram.com/images/equations/DoubleFactorial/Inline63.gif) |
(24) |
 |
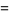 |
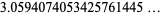 |
(25) |
(OEIS A143280), where 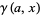 is a lower incomplete gamma function. This sum is a special case of the reciprocal multifactorial constant.
is a lower incomplete gamma function. This sum is a special case of the reciprocal multifactorial constant.
A closed-form sum due to Ramanujan is given by
![sum_(n=0)^infty(-1)^n[((2n-1)!!)/((2n)!!)]^3=[(Gamma(9/8))/(Gamma(5/4)Gamma(7/8))]^2](http://mathworld.wolfram.com/images/equations/DoubleFactorial/NumberedEquation9.gif) |
(26) |
(Hardy 1999, p. 106). Whipple (1926) gives a generalization of this sum (Hardy 1999, pp. 111-112).
REFERENCES:
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 544-545 and 547-548, 1985.
Cajori, F. A History of Mathematical Notations, Vol. 2. New York: Dover, 1993.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Meserve, B. E. "Double Factorials." Amer. Math. Monthly 55, 425-426, 1948.
Sloane, N. J. A. Sequences A000165/M1878, A001147/M3002, A006882/M0876, A114488, and A143280 in "The On-Line Encyclopedia of Integer Sequences."
Whipple, F. J. W. "On Well-Poised Series, Generalised Hypergeometric Series Having Parameters in Pairs, Each Pair with the Same Sum." Proc. London Math. Soc. 24, 247-263, 1926.



|
|
|
|
دور في الحماية من السرطان.. يجب تناول لبن الزبادي يوميا
|
|
|
|
|
|
|
العلماء الروس يطورون مسيرة لمراقبة حرائق الغابات
|
|
|
|
|
|
|
انطلاق الجلسة البحثية الرابعة لمؤتمر العميد العلمي العالمي السابع
|
|
|