Indefinite Integral
An integral of the form
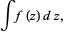 |
(1)
|
i.e., without upper and lower limits, also called an antiderivative. The first fundamental theorem of calculus allows definite integralsto be computed in terms of indefinite integrals. In particular, this theorem states that if 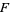 is the indefinite integral for a complex function
is the indefinite integral for a complex function 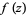 , then
, then
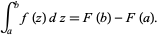 |
(2)
|
This result, while taught early in elementary calculus courses, is actually a very deep result connecting the purely algebraic indefinite integral and the purely analytic (or geometric) definite integral. Indefinite integration is implemented in the Wolfram Language as Integrate[f, z].
Since the derivative of a constant is zero, any constant may be added to an antiderivative and will still correspond to the same integral. Another way of stating this is that the antiderivative is a nonunique inverse of the derivative. For this reason, indefinite integrals are often written in the form
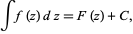 |
(3)
|
where 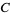 is an arbitrary constant known as the constant of integration. The Wolfram Language returns indefinite integrals without explicit constants of integration. This means that, depending on the form used for the integrand, antiderivatives
is an arbitrary constant known as the constant of integration. The Wolfram Language returns indefinite integrals without explicit constants of integration. This means that, depending on the form used for the integrand, antiderivatives 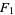 and
and 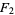 can be obtained that differ by a constant (or, more generally, a piecewise constant function). It also means that Integrate[f+g, z] may differ from Integrate[f, z] + Integrate[g, z] by an arbitrary (piecewise) constant.
can be obtained that differ by a constant (or, more generally, a piecewise constant function). It also means that Integrate[f+g, z] may differ from Integrate[f, z] + Integrate[g, z] by an arbitrary (piecewise) constant.
Note that indefinite integrals defined algebraically deal with complex quantities. However, many elementary calculus textbooks write formulas such as
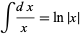 |
(4)
|
(where the notation  is used to indicate that
is used to indicate that  is assumed to be a real number) instead of the complex variable version
is assumed to be a real number) instead of the complex variable version
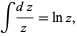 |
(5)
|
where 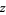 is generically a complex number (but also holds for real
is generically a complex number (but also holds for real 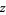 ). Defining a sort of "real-only" indefinite integral is perhaps done so that students can apply the first fundamental theorem of calculus using a Riemann integral and get correct answers while completely avoiding the use of complex analysis, multivalued functions, etc. (Although it should be noted that the first fundamental theorem of calculus only applies if the integrand is continuous on the interval of integration, so the additional stipulation must be made that
). Defining a sort of "real-only" indefinite integral is perhaps done so that students can apply the first fundamental theorem of calculus using a Riemann integral and get correct answers while completely avoiding the use of complex analysis, multivalued functions, etc. (Although it should be noted that the first fundamental theorem of calculus only applies if the integrand is continuous on the interval of integration, so the additional stipulation must be made that ![int_a^bdx/x=[ln|x|]_b^a](http://mathworld.wolfram.com/images/equations/IndefiniteIntegral/Inline10.gif) can be applied only if the interval
can be applied only if the interval ![[a,b]](http://mathworld.wolfram.com/images/equations/IndefiniteIntegral/Inline11.gif) does not contain 0.)
does not contain 0.)
However, this work (and the Wolfram Language) eschew the "real-only" definition, since inclusion of the absolute value means that the indefinite integral is no longer valid for a generic complex variable 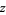 (the presence of the
(the presence of the 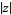 means the Cauchy-Riemann equations no longer can hold), and also violates the purely algebraic definition of indefinite integrals. Since physical problem involve definite integrals, it is much more sensible to stick with the usual complex/algebraic definitions of indefinite integration. In other words, while the Riemann integral
means the Cauchy-Riemann equations no longer can hold), and also violates the purely algebraic definition of indefinite integrals. Since physical problem involve definite integrals, it is much more sensible to stick with the usual complex/algebraic definitions of indefinite integration. In other words, while the Riemann integral
![int_(-2)^(-1)(dx)/x=[ln|x|]_(-2)^(-1)=0-ln2=-ln2](http://mathworld.wolfram.com/images/equations/IndefiniteIntegral/NumberedEquation6.gif) |
(6)
|
gives the correct answer (and avoids complex quantities along the way), so does the complex integral
![int_(-2)^(-1)(dz)/z=[lnz]_(-2)^(-1)=(ipi)-(ipi+ln2)=-ln2,](http://mathworld.wolfram.com/images/equations/IndefiniteIntegral/NumberedEquation7.gif) |
(7)
|
whereas the latter form preserves the benefits of genericness and at the same time prepares students for the extremely powerful tool of complex analysis which they should know about and will probably be learning about shortly in any case.
Liouville showed that the integrals
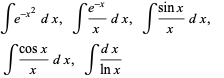 |
(8)
|
cannot be expressed in terms of a finite number of elementary functions. These give rise to the functions
(Havil 2003, p. 105), which are called erf, the exponential integral, sine integral, cosine integral, and logarithmic integral, respectively. The integral of any function of the form 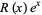 , where
, where 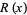 is a rational function, reduces to elementary integrals and the function
is a rational function, reduces to elementary integrals and the function 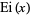 (Havil 2003, p. 106).
(Havil 2003, p. 106).
Other irreducibles include
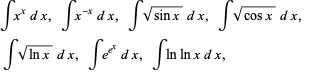 |
(14)
|
(cf. Marchisotto and Zakeri 1994), the last few of which can be written in closed form as
where 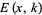 is an elliptic integral of the second kind,
is an elliptic integral of the second kind, 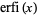 is the erfi function, and
is the erfi function, and 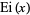 is the exponential integral.
is the exponential integral.
Chebyshev proved that if 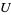 ,
, 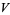 , and
, and 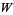 are rational numbers, then
are rational numbers, then
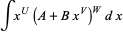 |
(20)
|
is integrable in terms of elementary functions iff 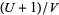 ,
, 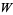 , or
, or 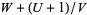 is an integer (Ritt 1948, Shanks 1993).
is an integer (Ritt 1948, Shanks 1993).
Integration for general input is a tricky problem for symbolic mathematics software. In fact, many simple indefinite integrals, such as
![int[d/(dz)Li_2(zlnz)]dz
=-int[((lnz+1)ln(1-zlnz))/(zlnz)]dz
int[d/(dz)(1/2sqrt(pi)erf(az)erf(bz))]dz
=int[be^(-b^2z^2)erf(az)+ae^(-a^2z^2)erf(bz)]dz,](http://mathworld.wolfram.com/images/equations/IndefiniteIntegral/NumberedEquation11.gif) |
(21)
|
where 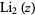 is the dilogarithm, cannot be done by very sophisticated software systems, including even the Wolfram Language.
is the dilogarithm, cannot be done by very sophisticated software systems, including even the Wolfram Language.
A selection of indefinite integrals are summarized below for power functions
trigonometric functions
combinations of trigonometric functions
inverse trigonometric functions
second-order rational functions and square roots
Jacobi elliptic functions
and the squares of Jacobi elliptic functions
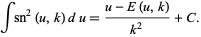 |
(55)
|
Here, 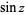 is the sine;
is the sine; 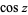 is the cosine;
is the cosine; 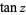 is the tangent;
is the tangent; 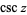 is the cosecant;
is the cosecant; 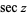 is the secant;
is the secant; 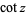 is the cotangent;
is the cotangent;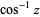 is the inverse cosine;
is the inverse cosine; 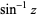 is the inverse sine;
is the inverse sine; 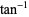 is the inverse tangent;
is the inverse tangent; 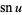 ,
, 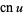 , and
, and 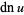 are Jacobi elliptic functions;
are Jacobi elliptic functions; 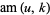 is the Jacobi amplitude;
is the Jacobi amplitude; 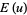 is a complete elliptic integral of the second kind; and
is a complete elliptic integral of the second kind; and 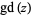 is the Gudermannian.
is the Gudermannian. 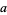 is assumed to be real and positive, and
is assumed to be real and positive, and 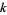 is the modulus.
is the modulus.
To derive (◇), let 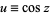 , so
, so 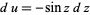 and
and
To derive (◇), let 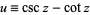 , so
, so 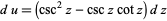 and
and
To derive (◇), let
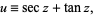 |
(67)
|
so
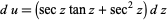 |
(68)
|
and
To derive (◇), let 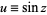 , so
, so 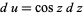 and
and
REFERENCES:
Boros, G. and Moll, V. Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals. Cambridge, England: Cambridge University Press, 2004.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.
Marchisotto, E. A. and Zakeri, G.-A. "An Invitation to Integration in Finite Terms." College Math. J. 25, 295-308, 1994.
Ritt, J. F. Integration in Finite Terms: Liouville's Theory of Elementary Methods. New York: Columbia University Press, 1948.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, 1993.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


