


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-10-2019
Date: 21-9-2018
Date: 5-9-2019
|
 |
 |
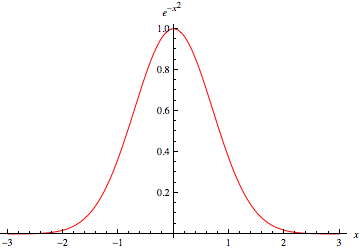
In one dimension, the Gaussian function is the probability density function of the normal distribution,
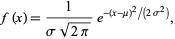 |
(1) |
sometimes also called the frequency curve. The full width at half maximum (FWHM) for a Gaussian is found by finding the half-maximum points 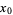 . The constant scaling factor can be ignored, so we must solve
. The constant scaling factor can be ignored, so we must solve
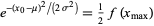 |
(2) |
But 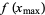 occurs at
occurs at 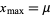 , so
, so
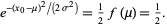 |
(3) |
Solving,
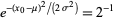 |
(4) |
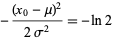 |
(5) |
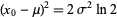 |
(6) |
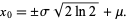 |
(7) |
The full width at half maximum is therefore given by
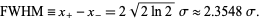 |
(8) |
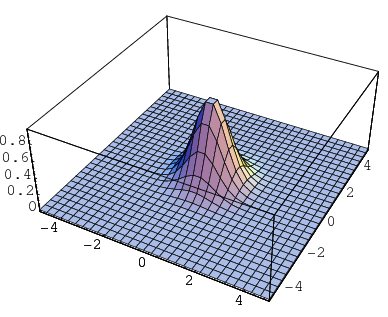
In two dimensions, the circular Gaussian function is the distribution function for uncorrelated variates 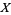 and
and 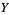 having a bivariate normal distribution and equal standard deviation
having a bivariate normal distribution and equal standard deviation 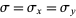 ,
,
![f(x,y)=1/(2pisigma^2)e^(-[(x-mu_x)^2+(y-mu_y)^2]/(2sigma^2)).](http://mathworld.wolfram.com/images/equations/GaussianFunction/NumberedEquation9.gif) |
(9) |
The corresponding elliptical Gaussian function corresponding to 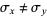 is given by
is given by
![f(x,y)=1/(2pisigma_xsigma_y)e^(-[(x-mu_x)^2/(2sigma_x^2)+(y-mu_y)^2/(2sigma_y^2)]).](http://mathworld.wolfram.com/images/equations/GaussianFunction/NumberedEquation10.gif) |
(10) |
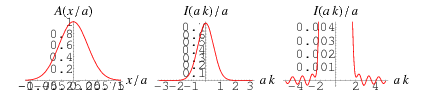
The Gaussian function can also be used as an apodization function
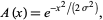 |
(11) |
shown above with the corresponding instrument function. The instrument function is
![I(k)=e^(-2pi^2k^2sigma^2)sigmasqrt(pi/2)[erf((a-2piiksigma^2)/(sigmasqrt(2)))+erf((a+2piiksigma^2)/(sigmasqrt(2)))],](http://mathworld.wolfram.com/images/equations/GaussianFunction/NumberedEquation12.gif) |
(12) |
which has maximum
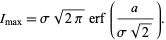 |
(13) |
As 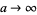 , equation (12) reduces to
, equation (12) reduces to
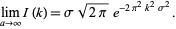 |
(14) |
The hypergeometric function is also sometimes known as the Gaussian function.
REFERENCES:
MacTutor History of Mathematics Archive. "Frequency Curve." http://www-groups.dcs.st-and.ac.uk/~history/Curves/Frequency.html.



|
|
|
|
دراسة: حفنة من الجوز يوميا تحميك من سرطان القولون
|
|
|
|
|
|
|
تنشيط أول مفاعل ملح منصهر يستعمل الثوريوم في العالم.. سباق "الأرنب والسلحفاة"
|
|
|
|
|
|
|
المجمع العلمي يقيم دورة تطويرية عن أساليب التدريس ويختتم أخرى تخص أحكام التلاوة
|
|
|