
 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-4-2019
Date: 4-8-2019
Date: 2-10-2019
|
Let the elliptic modulus 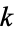 satisfy
satisfy 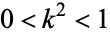 . (This may also be written in terms of the parameter
. (This may also be written in terms of the parameter 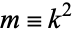 or modular angle
or modular angle 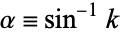 .) The incomplete elliptic integral of the second kind is then defined as
.) The incomplete elliptic integral of the second kind is then defined as
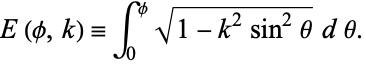 |
(1) |
The elliptic integral of the second kind is implemented in the Wolfram Language as EllipticE[phi, m] (note the use of the parameter 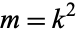 instead of the modulus
instead of the modulus 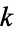 ).
).
The complete elliptic integral of the second kind 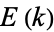 is defined by
is defined by
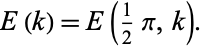 |
(2) |
To place the elliptic integral of the second kind in a slightly different form, let
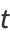 |
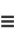 |
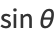 |
(3) |
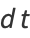 |
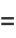 |
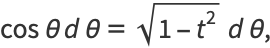 |
(4) |
so the elliptic integral can also be written as
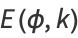 |
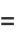 |
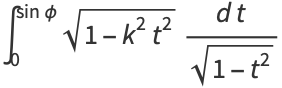 |
(5) |
 |
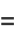 |
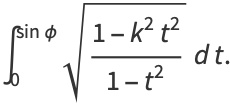 |
(6) |
A generalization replacing 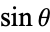 with
with 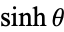 in (1) gives
in (1) gives
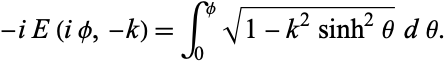 |
(7) |
The incomplete elliptic integral of the second kind of the form 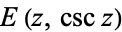 can be written in terms of complete elliptic integrals of the first
can be written in terms of complete elliptic integrals of the first 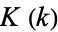 and second kinds
and second kinds 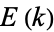 as
as
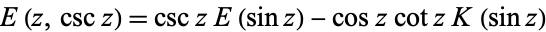 |
(8) |
for ![-pi/2<R[z]<pi/2](http://mathworld.wolfram.com/images/equations/EllipticIntegraloftheSecondKind/Inline25.gif) .
.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Elliptic Integrals." Ch. 17 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 587-607, 1972.
Spanier, J. and Oldham, K. B. "The Complete Elliptic Integrals 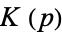 and
and 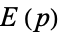 " and "The Incomplete Elliptic Integrals
" and "The Incomplete Elliptic Integrals 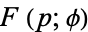 and
and 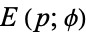 ." Chs. 61 and 62 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 609-633, 1987.
." Chs. 61 and 62 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 609-633, 1987.
Tölke, F. "Parameterfunktionen." Ch. 3 in Praktische Funktionenlehre, zweiter Band: Theta-Funktionen und spezielle Weierstraßsche Funktionen. Berlin: Springer-Verlag, pp. 83-115, 1966.
Tölke, F. "Umkehrfunktionen der Jacobischen elliptischen Funktionen und elliptische Normalintegrale erster Gattung. Elliptische Amplitudenfunktionen sowie Legendresche F- und E-Funktion. Elliptische Normalintegrale zweiter Gattung. Jacobische Zeta- und Heumansche Lambda-Funktionen," and "Normalintegrale dritter Gattung. Legendresche 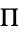 -Funktion. Zurückführung des allgemeinen elliptischen Integrals auf Normalintegrale erster, zweiter, und dritter Gattung." Chs. 6-7 in Praktische Funktionenlehre, dritter Band: Jacobische elliptische Funktionen, Legendresche elliptische Normalintegrale und spezielle Weierstraßsche Zeta- und Sigma Funktionen. Berlin: Springer-Verlag, pp. 58-144, 1967.
-Funktion. Zurückführung des allgemeinen elliptischen Integrals auf Normalintegrale erster, zweiter, und dritter Gattung." Chs. 6-7 in Praktische Funktionenlehre, dritter Band: Jacobische elliptische Funktionen, Legendresche elliptische Normalintegrale und spezielle Weierstraßsche Zeta- und Sigma Funktionen. Berlin: Springer-Verlag, pp. 58-144, 1967.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|