Spherical Bessel Function of the Second Kind

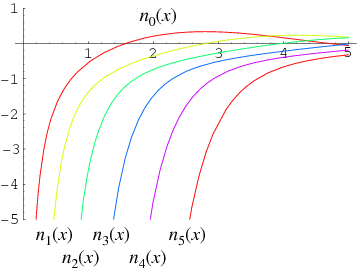
The spherical Bessel function of the second kind, denoted 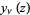 or 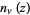, is defined by

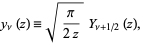(1)

where 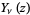 is a Bessel function of the second kind and, in general,  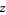and  are complex numbers.

The spherical Bessel function of the second kind is implemented in the Wolfram Language as SphericalBesselY[n,z].

The function is most commonly encountered in the case 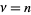 an integer, in which case it is given by

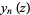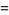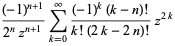			(2)
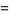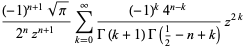			(3)
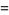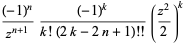			(4)
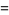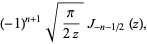			(5)

where 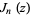 is a Bessel function of the first kind.

Specific cases for small nonnegative 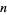 are given by

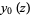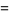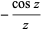			(6)
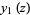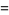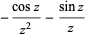			(7)
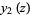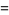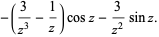			(8)

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Spherical Bessel Functions." §10.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 437-442, 1972.

Arfken, G. "Spherical Bessel Functions." §11.7 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 622-636, 1985.