
Modified Spherical Bessel Function of the Second Kind
 المؤلف:
Abramowitz, M. and Stegun, I. A.
المؤلف:
Abramowitz, M. and Stegun, I. A.
 المصدر:
"Modified Spherical Bessel Functions." §10.2 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
المصدر:
"Modified Spherical Bessel Functions." §10.2 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
 الجزء والصفحة:
...
الجزء والصفحة:
...
 25-3-2019
25-3-2019
 2476
2476
Modified Spherical Bessel Function of the Second Kind
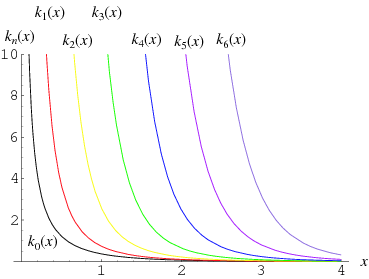
A modified spherical Bessel function of the second kind, also called a "spherical modified Bessel function of the first kind" (Arfken 1985) or (regrettably) a "modified spherical Bessel function of the third kind" (Abramowitz and Stegun 1972, p. 443), is the second solution to the modified spherical Bessel differential equation, given by
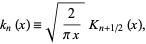 |
(1)
|
where 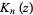 is a modified Bessel function of the second kind (Arfken 1985, p. 633)
is a modified Bessel function of the second kind (Arfken 1985, p. 633)
For positive  , the first few values for small nonnegative integer indices are
, the first few values for small nonnegative integer indices are
(OEIS A001498).
Writing
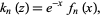 |
(7)
|
the 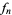 are given by the recurrence equation
are given by the recurrence equation
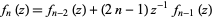 |
(8)
|
together with
(Abramowitz and Stegun 1972, p. 444).
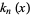 has no definite parity (Arfken 1985, p. 633).
has no definite parity (Arfken 1985, p. 633).
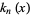 is related to the spherical Hankel function of the first kind
is related to the spherical Hankel function of the first kind 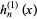 by
by
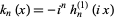 |
(11)
|
for 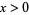 and integer
and integer 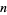 (Arfken 1985, p. 633).
(Arfken 1985, p. 633).
They also satisfy the differential identities
and the recurrence relations
(Arfken 1985, p. 634).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Modified Spherical Bessel Functions." §10.2 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 443-445, 1972.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 663-634, 1985.
Sloane, N. J. A. Sequence A001498 in "The On-Line Encyclopedia of Integer Sequences."
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


