المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر
أضيف حديثاً
نوعيات نشاط طلوقة الماشية Types of bull activities
2024-11-01
طـرق تقـليـل العـمالـة فـي المنظمـات
2024-11-01
التبويض Ovulation والهياج الجنسي heat والشبق estrous لدى الابقار
2024-11-01
فسيولوجيا تكوين المني في الماشية
2024-11-01
خـطوات تـقلـيل العـمالـة فـي المنظمـة
2024-11-01
مـزايـا ومـسـاوئ تـقليـل العـمالـة فـي المنظمـات
2024-11-01

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
عنَّف الله المجرمين وذكر عقوبتهم
2-12-2015
أبو دقيق الخبيزة Vanessa cardui (L.)
3-4-2018
goal (n.)
2023-09-13
Interacting processes
29-3-2022
حكم من زاد على الرباعية خامسة سهوا.
10-1-2016
المبيدات الميكروبية
10-12-2015

Bessel Function Neumann Series  
  
1204   02:09 مساءً   date: 24-3-2019
Author : Watson, G. N
Book or Source : A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University Press, 1966.
Page and Part : ...


Read More
Gamma Product
Date: 22-5-2019 1116
Square Integrable
Date: 19-5-2018 1931
Inverse Hyperbolic Functions
Date: 3-6-2019 4344

Bessel Function Neumann Series
A series of the form

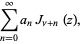sum_(n=0)^inftya_nJ_(nu+n)(z),

(1)

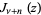where nu is a real and J_(nu+n)(z) is a Bessel function of the first kind. Special cases are

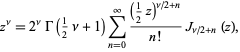z^nu=2^nuGamma(1/2nu+1)sum_(n=0)^infty((1/2z)^(nu/2+n))/(n!)J_(nu/2+n)(z),

(2)

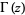where Gamma(z) is the gamma function, and

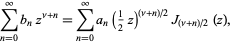sum_(n=0)^inftyb_nz^(nu+n)=sum_(n=0)^inftya_n(1/2z)^((nu+n)/2)J_((nu+n)/2)(z),

(3)

where

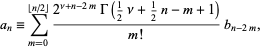a_n=sum_(m=0)^(|_n/2_|)(2^(nu+n-2m)Gamma(1/2nu+1/2n-m+1))/(m!)b_(n-2m),

(4)

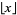and |_x_| is the floor function.

REFERENCES:

Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University Press, 1966.




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
التاريخ / 2024-10-29

الأخبار العلمية
سر الجهاز المناعي الفتي!
التاريخ / 2024-10-29

الساحة الاسلامية
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
التاريخ / 2024-10-31