Bessel Function
المؤلف:
Adamchik, V.
المصدر:
"The Evaluation of Integrals of Bessel Functions via G-Function Identities." J. Comput. Appl. Math. 64
الجزء والصفحة:
...
24-3-2019
3819
Bessel Function
A function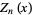 
defined by the recurrence relations
 |
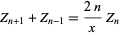(1)
|
and
 |
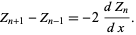(2)
|
The Bessel functions are more frequently defined as solutions to the differential equation
 |
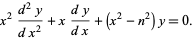(3)
|
There are two classes of solution, called the Bessel function of the first kind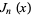 
and Bessel function of the second kind 
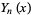. (A Bessel function of the third kind, more commonly called a Hankel function, is a special combination of the first and second kinds.) Several related functions are also defined by slightly modifying the defining equations.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Bessel Functions of Integer Order," "Bessel Functions of Fractional Order," and "Integrals of Bessel Functions." Chs. 9-11 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 355-389, 435-456, and 480-491, 1972.
Adamchik, V. "The Evaluation of Integrals of Bessel Functions via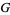 
-Function Identities." J. Comput. Appl. Math. 64, 283-290, 1995.
Arfken, G. "Bessel Functions." Ch. 11 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 573-636, 1985.
Bickley, W. G. Bessel Functions and Formulae. Cambridge, England: Cambridge University Press, 1957.
Bowman, F. Introduction to Bessel Functions. New York: Dover, 1958.
Byerly, W. E. "Cylindrical Harmonics (Bessel's Functions)." Ch. 7 in An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, pp. 219-237, 1959.
Gray, A. and Mathews, G. B. A Treatise on Bessel Functions and Their Applications to Physics, 2nd ed. New York: Dover, 1966.
Luke, Y. L. Integrals of Bessel Functions. New York: McGraw-Hill, 1962.
McLachlan, N. W. Bessel Functions for Engineers, 2nd ed. with corrections. Oxford, England: Clarendon Press, 1961.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Bessel Functions of Integral Order" and "Bessel Functions of Fractional Order, Airy Functions, Spherical Bessel Functions." §6.5 and 6.7 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 223-229 and 234-245, 1992.
Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University Press, 1966.
Weisstein, E. W. "Books about Bessel Functions." http://www.ericweisstein.com/encyclopedias/books/BesselFunctions.html.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
