Generalized Fourier Integral

The so-called generalized Fourier integral is a pair of integrals--a "lower Fourier integral" and an "upper Fourier integral"--which allow certain complex-valued functions 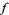 to be decomposed as the sum of integral-defined functions, each of which resembles the usual Fourier integral associated to  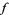and maintains several key properties thereof.

Let  be a real variable, let 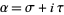 be a complex variable, and let  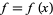be a function for which  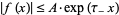as 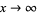, for which  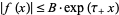as 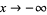, and for which  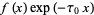has an analytic Fourier integral where here,  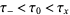are finite real constants. Next, define the upper and lower generalized Fourier integrals  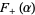and 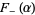 associated to 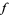, respectively, by

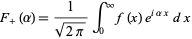(1)

and

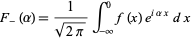(2)

on the complex regions 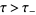 and 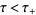, respectively. Then, for  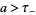and ,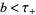

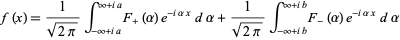(3)

where the first integral summand equals 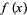 for 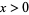 and is zero for  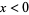while the second integral summand is zero for  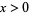and equals  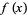for 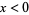. The decomposition () is called the generalized Fourier integral corresponding to .

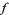Note that some literature defines the upper and lower integrals 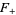 and 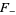 with multiplicative constants different from 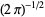, whereby the identity in () may look slightly different.

REFERENCES:

Linton, C. M. and McIver, P. Handbook of Mathematical Techniques for Wave/Structure Interactions. Boca Raton, FL: CRC Press, 2001.

Noble, B. Methods Based on the Wiener-Hopf Technique For the Solution of Partial Differential Equations. Belfast, Northern Ireland: Pergamon Press, 1958.