
Entire Function
 المؤلف:
Knopp, K
المؤلف:
Knopp, K
 المصدر:
Entire Transcendental Functions." Ch. 9 in Theory of Functions Parts I and II, Two Volumes Bound as One, Part I.New York: Dover
المصدر:
Entire Transcendental Functions." Ch. 9 in Theory of Functions Parts I and II, Two Volumes Bound as One, Part I.New York: Dover
 الجزء والصفحة:
...
الجزء والصفحة:
...
 18-11-2018
18-11-2018
 928
928
Entire Function
If a complex function is analytic at all finite points of the complex plane 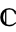 , then it is said to be entire, sometimes also called "integral" (Knopp 1996, p. 112).
, then it is said to be entire, sometimes also called "integral" (Knopp 1996, p. 112).
Any polynomial 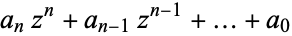 is entire.
is entire.
Examples of specific entire functions are given in the following table.
| function |
symbol |
| Airy functions |
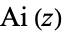 , , 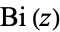 |
| Airy function derivatives |
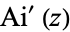 , , 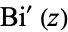 |
| Anger function |
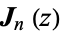 |
| Barnes G-function |
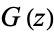 |
| bei |
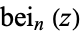 |
| ber |
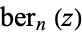 |
| Bessel function of the first kind |
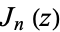 |
| Bessel function of the second kind |
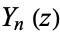 |
| Beurling's function |
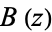 |
| cosine |
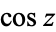 |
| coversine |
 |
| Dawsons integral |
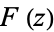 |
| erf |
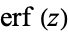 |
| erfc |
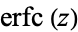 |
| erfi |
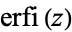 |
| exponential function |
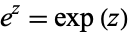 |
| Fresnel integrals |
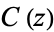 , , 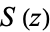 |
| gamma function reciprocal |
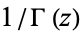 |
| generalized hypergeometric function |
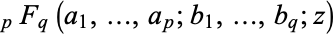 |
| haversine |
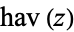 |
| hyperbolic cosine |
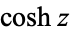 |
| hyperbolic sine |
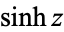 |
| Jacobi elliptic functions |
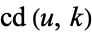 , , 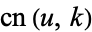 , , 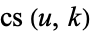 , , 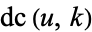 , , 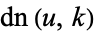 , , 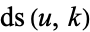 , , 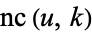 , , 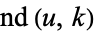 , , 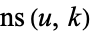 , , 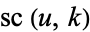 , , 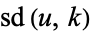 , , 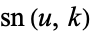 |
| Jacobi theta functions |
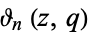 |
| Jacobi theta function derivatives |
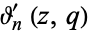 |
| Mittag-Leffler function |
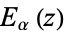 |
| modified Struve function |
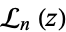 |
| Neville theta functions |
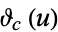 , , 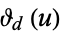 , , 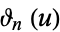 , , 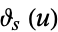 |
| Shi |
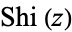 |
| sine |
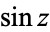 |
| sine integral |
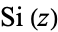 |
| spherical Bessel function of the first kind |
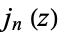 |
| Struve function |
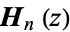 |
| versine |
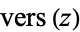 |
| Weber functions |
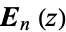 |
| Wright function |
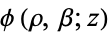 |
| xi-function |
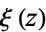 |
Liouville's boundedness theorem states that a bounded entire function must be a constant function.
REFERENCES:
Knopp, K. "Entire Transcendental Functions." Ch. 9 in Theory of Functions Parts I and II, Two Volumes Bound as One, Part I.New York: Dover, pp. 112-116, 1996.
Krantz, S. G. "Entire Functions and Liouville's Theorem." §3.1.3 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 31-32, 1999.
 الاكثر قراءة في التحليل العقدي
الاكثر قراءة في التحليل العقدي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


