Conformal Mapping
A conformal mapping, also called a conformal map, conformal transformation, angle-preserving transformation, or biholomorphic map, is a transformation  that preserves local angles. An analytic function is conformal at any point where it has a nonzero derivative. Conversely, any conformal mapping of a complex variable which has continuous partial derivatives is analytic. Conformal mapping is extremely important in complex analysis, as well as in many areas of physics and engineering.
that preserves local angles. An analytic function is conformal at any point where it has a nonzero derivative. Conversely, any conformal mapping of a complex variable which has continuous partial derivatives is analytic. Conformal mapping is extremely important in complex analysis, as well as in many areas of physics and engineering.
A mapping that preserves the magnitude of angles, but not their orientation is called an isogonal mapping (Churchill and Brown 1990, p. 241).
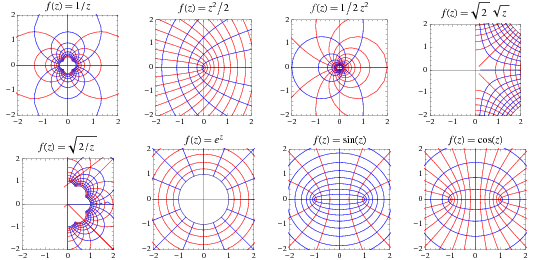

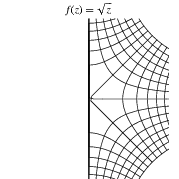
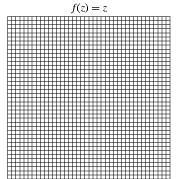
Several conformal transformations of regular grids are illustrated in the first figure above. In the second figure above, contours of constant 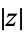 are shown together with their corresponding contours after the transformation. Moon and Spencer (1988) and Krantz (1999, pp. 183-194) give tables of conformal mappings.
are shown together with their corresponding contours after the transformation. Moon and Spencer (1988) and Krantz (1999, pp. 183-194) give tables of conformal mappings.
A method due to Szegö gives an iterative approximation to the conformal mapping of a square to a disk, and an exact mapping can be done using elliptic functions (Oberhettinger and Magnus 1949; Trott 2004, pp. 71-77).
Let 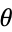 and
and 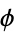 be the tangents to the curves
be the tangents to the curves 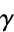 and
and 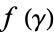 at
at 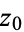 and
and 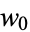 in the complex plane,
in the complex plane,
![arg(w-w_0)=arg[(f(z)-f(z_0))/(z-z_0)]+arg(z-z_0).](http://mathworld.wolfram.com/images/equations/ConformalMapping/NumberedEquation1.gif) |
(3)
|
Then as 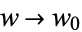 and
and 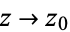 ,
,
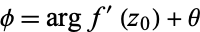 |
(4)
|
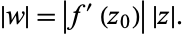 |
(5)
|
A function 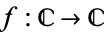 is conformal iff there are complex numbers
is conformal iff there are complex numbers 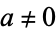 and
and 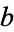 such that
such that
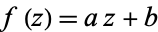 |
(6)
|
for 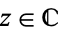 (Krantz 1999, p. 80). Furthermore, if
(Krantz 1999, p. 80). Furthermore, if 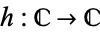 is an analytic function such that
is an analytic function such that
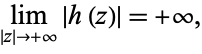 |
(7)
|
then 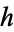 is a polynomial in
is a polynomial in 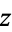 (Greene and Krantz 1997; Krantz 1999, p. 80).
(Greene and Krantz 1997; Krantz 1999, p. 80).
Conformal transformations can prove extremely useful in solving physical problems. By letting 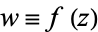 , the real and imaginary parts of
, the real and imaginary parts of 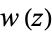 must satisfy the Cauchy-Riemann equations and Laplace's equation, so they automatically provide a scalar potentialand a so-called stream function. If a physical problem can be found for which the solution is valid, we obtain a solution--which may have been very difficult to obtain directly--by working backwards.
must satisfy the Cauchy-Riemann equations and Laplace's equation, so they automatically provide a scalar potentialand a so-called stream function. If a physical problem can be found for which the solution is valid, we obtain a solution--which may have been very difficult to obtain directly--by working backwards.
For example, let
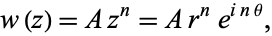 |
(8)
|
the real and imaginary parts then give

For 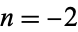 ,
,
which is a double system of lemniscates (Lamb 1945, p. 69).

For 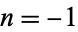 ,
,
This solution consists of two systems of circles, and 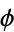 is the potential function for two parallel opposite charged line charges (Feynman et al. 1989, §7-5; Lamb 1945, p. 69).
is the potential function for two parallel opposite charged line charges (Feynman et al. 1989, §7-5; Lamb 1945, p. 69).
For 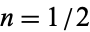 ,
,
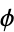 gives the field near the edge of a thin plate (Feynman et al. 1989, §7-5).
gives the field near the edge of a thin plate (Feynman et al. 1989, §7-5).
For 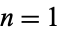 ,
,
giving two straight lines (Lamb 1945, p. 68).

For 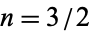 ,
,
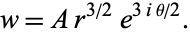 |
(19)
|
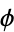 gives the field near the outside of a rectangular corner (Feynman et al. 1989, §7-5).
gives the field near the outside of a rectangular corner (Feynman et al. 1989, §7-5).

For 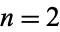 ,
,
These are two perpendicular hyperbolas, and 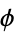 is the potential function near the middle of two point charges or the field on the opening side of a charged right angle conductor (Feynman 1989, §7-3).
is the potential function near the middle of two point charges or the field on the opening side of a charged right angle conductor (Feynman 1989, §7-3).
REFERENCES:
Arfken, G. "Conformal Mapping." §6.7 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 392-394, 1985.
Bergman, S. The Kernel Function and Conformal Mapping. New York: Amer. Math. Soc., 1950.
Carathéodory, C. Conformal Representation. New York: Dover, 1998.
Carrier, G.; Crook, M.; and Pearson, C. E. Functions of a Complex Variable: Theory and Technique. New York: McGraw-Hill, 1966.
Churchill, R. V. and Brown, J. W. Complex Variables and Applications, 5th ed. New York: McGraw-Hill, 1990.
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., p. 80, 1967.
Feynman, R. P.; Leighton, R. B.; and Sands, M. The Feynman Lectures on Physics, Vol. 2. Redwood City, CA: Addison-Wesley, 1989.
Greene, R. E. and Krantz, S. G. Function Theory of One Complex Variable. New York: Wiley, 1997.
Katznelson, Y. An Introduction to Harmonic Analysis. New York: Dover, 1976.
Kober, H. Dictionary of Conformal Representations. New York: Dover, 1957.
Krantz, S. G. "Conformality," "The Geometric Theory of Holomorphic Functions," "Applications That Depend on Conformal Mapping," and "A Pictorial Catalog of Conformal Maps." §2.2.5, Ch. 6, Ch. 14, and Appendix to Ch. 14 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 25, 79-88, and 163-194, 1999.
Kythe, P. K. Computational Conformal Mapping. Boston, MA: Birkhäuser, 1998.
Lamb, H. Hydrodynamics, 6th ed. New York: Dover, 1945.
Mathews, J. "Conformal Mappings." http://www.ecs.fullerton.edu/~mathews/fofz/cmaps.html.
Moon, P. and Spencer, D. E. "Conformal Transformations." §2.01 in Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions, 2nd ed. New York: Springer-Verlag, pp. 49-76, 1988.
Morse, P. M. and Feshbach, H. "Conformal Mapping." §4.7 in Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 358-362 and 443-453, 1953.
Nehari, Z. Conformal Mapping. New York: Dover, 1982.
Oberhettinger, F. and Magnus, W. Anwendungen der elliptischen Funktionen in Physik and Technik. Berlin: Springer-Verlag, 1949.
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, 2004. http://www.mathematicaguidebooks.org/.
 الاكثر قراءة في التحليل العقدي
الاكثر قراءة في التحليل العقدي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


