


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-10-2018
Date: 25-11-2018
Date: 16-12-2018
|
Let 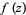 be a transcendental meromorphic function, and let
be a transcendental meromorphic function, and let 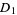 ,
, 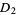 , ...,
, ..., 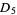 be five simply connected domains in
be five simply connected domains in 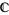 with disjoint closures (Ahlfors 1932). Then there exists
with disjoint closures (Ahlfors 1932). Then there exists 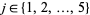 and, for any
and, for any 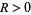 , a simply connected domain
, a simply connected domain 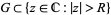 such that
such that 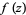 is a conformal mapping of
is a conformal mapping of 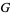 onto
onto 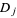 . If
. If 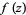 has only finitely many poles, then "five" may be replaced by "three" (Ahlfors 1933).
has only finitely many poles, then "five" may be replaced by "three" (Ahlfors 1933).
REFERENCES:
Ahlfors, L. "Sur les fonctions inverses des fonctions méromorphes." Comptes Rendus Acad. Sci. Paris 194, 1145-1147, 1932. Reprinted in Lars Valerian Ahlfors: Collected Papers Volume 1, 1929-1955 (Ed. R. M. Shortt). Boston, MA: Birkhäuser, 149-151, 1982.
Ahlfors, L. "Über die Kreise die von einer Riemannschen Fläche schlicht überdeckt werden." Comm. Math. Helv. 5, 28-38, 1933. Reprinted in Lars Valerian Ahlfors: Collected Papers Volume 1, 1929-1955 (Ed. R. M. Shortt). Boston, MA: Birkhäuser, 163-173, 1982.
Bergweiler, W. "Iteration of Meromorphic Functions." Bull. Amer. Math. Soc. (N. S.) 29, 151-188, 1993.
Hayman, W. K. Meromorphic Functions. Oxford, England: Oxford University Press, 1964.
Nevanlinna, R. Analytic Functions. New York: Springer-Verlag, 1970.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|