"The" imaginary number 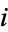 (also called the imaginary unit) is defined as the square root of 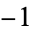, i.e., 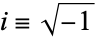. Although there are two possible square roots of any number, the square roots of a negative number cannot be distinguished until one of the two is defined as the imaginary unit, at which point  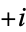and 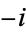 can then be distinguished. Since either choice is possible, there is no ambiguity in defining  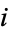as "the" square root of .

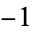In the Wolfram Language, the imaginary number is implemented as I. For some reason, engineers and physicists prefer the symbol j to 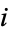, probably because the symbol  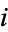(or 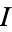) is commonly used to denote current.

In the novel The Da Vinci Code, the character Robert Langdon jokes that character Sophie Neveu "believes in the imaginary number 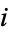 because it helps her break code" (Brown 2003, p. 351). In the movie Proof (2005), the character Hal Dobbs (played by Jake Gyllenhaal) is a mathematics graduate student whose rock-and-roll band "plays" a song called "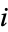." The joke is that when the band "plays" the song, they remain silent and motionless for several minutes since the song is "imaginary." In Isaac Asimov's short story "The Imaginary" (1942), eccentric psychologist Tan Porus explains the behavior of a mysterious species of squid by using imaginary numbers in the equations which describe its psychology. The anthology Imaginary Numbers: An Anthology of Marvelous Mathematical Stories, Diversions, Poems, and Musings (Frucht 2000) includes many other works involving imaginary numbers.

Numbers of the form 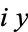, where  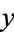is a real number, are called imaginary numbers (or sometimes, for emphasis, purely imaginary numbers). Numbers of the form  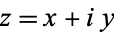where 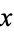 and 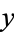 are real numbers are called complex numbers, and when  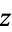is used to denote a complex number, it is sometimes (in older texts) called an "affix."

The square root of 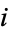 is

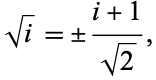(1)

since

(2)

This can be immediately derived from the Euler formula with ,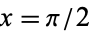

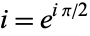(3)

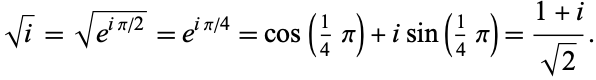(4)

Amazingly, the principal value of 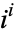 is a real number given by

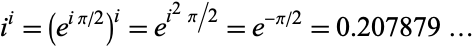(5)

(OEIS A049006; Uhler 1921; Wells 1986, p. 26; Derbyshire 2004, p. 205).

Interestingly, all higher-order power towers have complex values, but the infinite power tower converges to the value

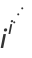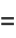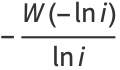			(6)
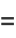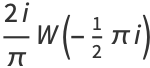			(7)
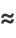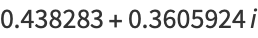			(8)

(OEIS A077589 and A077590; Macintyre 1966), where 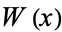 is the Lambert W-function, as illustrated above.

The following mathematical joke exhibits the strange way in which mathematicians think. "Rrrrrring. Operator: I'm sorry, the number you have dialed is imaginary. Please multiply by 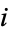 and dial again." A variant of this joke, actually left on one mathematician's phone by his son states, "I'm sorry, the number you have dialed is an imaginary number. Please rotate by  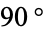and try again." Taking this joke one step further gives the "identity"

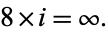(9)

REFERENCES:

Asimov, I. "The Imaginary." Super Science Stories. Nov. 1942. Reprinted in The Early Asimov, Book One. Del Rey, pp. 246-262, 1986.

Brown, D. The Da Vinci Code. New York: Doubleday, 2003.

Courant, R. and Robbins, H. What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, p. 89, 1996.

Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.

Frucht, W. (Ed.). Imaginary Numbers: An Anthology of Marvelous Mathematical Stories, Diversions, Poems, and Musings, 2nd ed. New York: Wiley, 2000.

Nahin, P. J. An Imaginary Tale: The Story of -1. Princeton, NJ: Princeton University Press, 2007.

Macintyre, A. J. "Convergence of 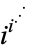." Proc. Amer. Math. Soc. 17, 67, 1966.

Mazur, B. Imagining Numbers (Particularly the Square Root of Minus Fifteen). New York: Farrar, Straus and Giroux, 2003.

Sloane, N. J. A. Sequences A049006, A077589, and A077590 in "The On-Line Encyclopedia of Integer Sequences."

Uhler, S. "On the Numerical Value of 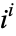." Amer. Math. Monthly 28, 114-116, 1921.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 26, 1986.

اخر الاخبار

اخبار العتبة العباسية المقدسة

المجمع العلمي يواصل إقامة مسابقة الثقلين القرآنية لطلبة مدارس كربلاء

عضو مجلس إدارة العتبة العباسية المقدسة يطلع على آليات تطوير البرامج التعليمية في مجموعة العميد

مجموعة مناحل الكفيل تختتم مشاركتها في معرض السليمانية الدولي للزراعة والصناعات الغذائية

لتوثيق التراث العلمي.. وفد قسم شؤون المعارف يلتقي عددًا من أعلام مدينة النجف

المزيد

الآخبار الصحية

ثورة طبية.. الذكاء الاصطناعي يكشف سرطان الكلى في وقت قياسي

لتعزيز الطاقة والتغلب على التعب.. عليك بـ7 طرق بسيطة

لتحسين الهضم والتحكم في الشهية.. ما أفضل وقت لتناول التمر؟

خبراء يكشفون تأثير الاستحمام في الظلام على جودة النوم !

المزيد

الآخبار التكنلوجية

إزالة ثاني أكسيد الكربون من الغلاف الجوي.. ما دور المحيطات والبحار؟

نظائر الهيليوم مقياس لاكتشاف رواسب الذهب.. كيف ذلك؟

الصين تطلق أول ناقلة نفط خام ذكية في العالم تعمل بالميثانول

الزمن على المريخ أسرع من الأرض.. دراسة علمية تكشف الفوارق

المزيد