المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر المرجع الالكتروني للمعلوماتية

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024


Quadratic Integral  
  
2326   08:15 مساءً   date: 17-9-2018
Author : Gradshteyn, I. S. and Ryzhik, I. M
Book or Source : Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.
Page and Part : ...


Read More
Pathological
Date: 16-5-2018 1999
Lehmer,s Constant
Date: 13-10-2019 1690
Path Integral
Date: 25-8-2018 1770

Quadratic Integral

To compute an integral of the form

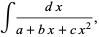int(dx)/(a+bx+cx^2),

(1)

complete the square in the denominator to obtain

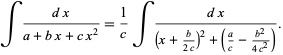int(dx)/(a+bx+cx^2)=1/cint(dx)/((x+b/(2c))^2+(a/c-(b^2)/(4c^2))).

(2)

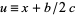Let u=x+b/2c. Then define

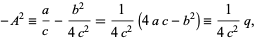-A^2=a/c-(b^2)/(4c^2)=1/(4c^2)(4ac-b^2)=1/(4c^2)q,

(3)

where

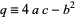q=4ac-b^2

(4)

is the negative of the polynomial discriminant. If 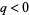q<0, then

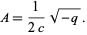A=1/(2c)sqrt(-q).

(5)

Now use partial fraction decomposition,

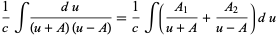1/cint(du)/((u+A)(u-A))=1/cint((A_1)/(u+A)+(A_2)/(u-A))du

(6)
((A_1)/(u+A)+(A_2)/(u-A))=(A_1(u-A)+A_2(u+A))/(u^2-A^2) =((A_1+A_2)u+A(A_2-A_1))/(u^2-A^2),

(7)

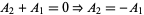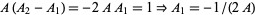so A_2+A_1=0=>A_2=-A_1 and A(A_2-A_1)=-2AA_1=1=>A_1=-1/(2A). Plugging these in,

1/cint(-1/(2A)1/(u+A)+1/(2A)1/(u-A))du =1/(2Ac)[-ln(u+A)+ln(u-A)] =1/(2Ac)ln((u-A)/(u+A)) =1/(2(1/(2c))sqrt(-q)c)ln((x+b/(2c)-1/(2c)sqrt(-q))/(x+b/(2c)+1/(2c)sqrt(-q))) =1/(sqrt(-q))ln((2cx+b-sqrt(-q))/(2cx+b+sqrt(-q)))

(8)

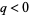for q<0. Note that this integral is also tabulated in Gradshteyn and Ryzhik (2000, equation 2.172), where it is given with a sign flipped.

REFERENCES:

Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
التاريخ / 2025-04-16

الأخبار العلمية
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
التاريخ / 2025-04-16

الساحة الاسلامية
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
التاريخ / 2025-04-14