


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-7-2018
Date: 12-7-2018
Date: 23-7-2018
|
The partial differential equation
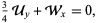 |
(1) |
where
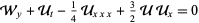 |
(2) |
(Krichever and Novikov 1980; Novikov 1999). Zwillinger (1997, p. 131) and Calogero and Degasperis (1982, p. 54) give the equation as
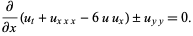 |
(3) |
The modified Kadomtsev-Petviashvili equation is given by
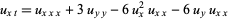 |
(4) |
(Clarkson 1986; Zwillinger 1997, p. 133).
REFERENCES:
Baker, H. F. Abelian Functions: Abel's Theorem and the Allied Theory, Including the Theory of the Theta Functions. New York: Cambridge University Press, p. xix, 1995.
Calogero, F. and Degasperis, A. Spectral Transform and Solitons: Tools to Solve and Investigate Nonlinear Evolution Equations.New York: North-Holland, 1982.
Clarkson, P. A. "The Painlevé Property, a Modified Boussinesq Equation and a Modified Kadomtsev-Petviashvili Equation." Physica D 19, 447-450, 1986.
Krichever, I. M. and Novikov, S. P. "Holomorphic Bundles over Algebraic Curves, and Nonlinear Equations." Russ. Math. Surv. 35, 53-80, 1980. English translation of Uspekhi Mat. Nauk 35, 47-68, 1980.
Novikov, D. P. "Algebraic-Geometric Solutions of the Krichever-Novikov Equation." Theoret. Math. Phys. 121, 1567-15773, 1999.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 131, 1997.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|