المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Kadomtsev-Petviashvili-Burgers Equation |
 1887
 02:48 مساءً
date: 21-7-2018 |
Author : Brugarino, T. 
Book or Source : "Similarity Solutions of the Generalized Kadomtsev-Petviashvili-Burgers Equation." Nuovo Cimento B 92 
Page and Part : ...|
Read More
Date: 13-7-2018
1774
Date: 13-7-2018
1091
Date: 13-7-2018
950
|
The so-called generalized Kadomtsev-Petviashvili-Burgers equation is the partial differential equation
 |
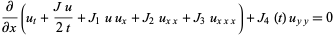(Brugarino 1986; Zwillinger 1997, p. 131).
REFERENCES:
Brugarino, T. "Similarity Solutions of the Generalized Kadomtsev-Petviashvili-Burgers Equation." Nuovo Cimento B 92, 142-156, 1986.
Dryuma, V. "On an Analytic Solution of the Two-Dimensional Korteweg-de Vries (KdV) Equation." Pisma v. ZhETF 19, 753-755, 1974. Reprinted in JETP Lett. 19, 387-388, 1974.
Infeld, E. and Rowlands, G. "An Example: The Kadomtsev-Petviashvili Equation." §7.10.4 in Nonlinear Waves, Solitons, and Chaos, 2nd ed. Cambridge, England: Cambridge University Press, pp. 196-199, 2000.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 131, 1997.
|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
الزائرون يحيون ليلة الجمعة الأخيرة من شهر ربيع الآخر عند مرقد أبي الفضل العبّاس (عليه السلام)
|
|
|
