Painlevé Property

Following the work of Fuchs in classifying first-order ordinary differential equations, Painlevé studied second-order ordinary differential equation of the form

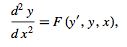
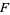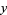where  is analytic in  and rational in  and 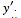 Painlevé found 50 types whose only movable singularities are ordinary poles. This characteristic is known as the Painlevé property. Six of the transcendents define new transcendents known as Painlevé transcendents, and the remaining 44 can be integrated in terms of classical transcendents, quadratures, or the Painlevé transcendents.

REFERENCES:

Slavyanov, S. Yu. and Lay, W. "Painlevé Property." §5.1 in Special Functions: A Unified Theory Based on Singularities. Oxford, England: Oxford University Press, pp. 232-236, 2000.