
Lotka-Volterra Equations
 المؤلف:
Boyce, W. E. and DiPrima, R. C
المؤلف:
Boyce, W. E. and DiPrima, R. C
 المصدر:
Elementary Differential Equations and Boundary Value Problems, 5th ed. New York: Wiley
المصدر:
Elementary Differential Equations and Boundary Value Problems, 5th ed. New York: Wiley
 الجزء والصفحة:
...
الجزء والصفحة:
...
 22-6-2018
22-6-2018
 1371
1371
Lotka-Volterra Equations
The Lotka-Volterra equations describe an ecological predator-prey (or parasite-host) model which assumes that, for a set of fixed positive constants 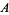 (the growth rate of prey),
(the growth rate of prey), 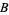 (the rate at which predators destroy prey),
(the rate at which predators destroy prey), 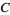 (the death rate of predators), and
(the death rate of predators), and 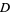 (the rate at which predators increase by consuming prey), the following conditions hold.
(the rate at which predators increase by consuming prey), the following conditions hold.
1. A prey population  increases at a rate
increases at a rate 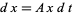 (proportional to the number of prey) but is simultaneously destroyed by predators at a rate
(proportional to the number of prey) but is simultaneously destroyed by predators at a rate 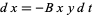 (proportional to the product of the numbers of prey and predators).
(proportional to the product of the numbers of prey and predators).
2. A predator population 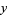 decreases at a rate
decreases at a rate 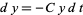 (proportional to the number of predators), but increases at a rate
(proportional to the number of predators), but increases at a rate 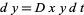 (again proportional to the product of the numbers of prey and predators).
(again proportional to the product of the numbers of prey and predators).
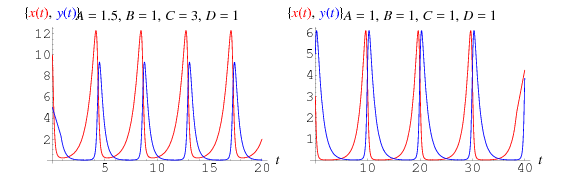
This gives the coupled differential equations
solutions of which are plotted above, where prey are shown in red, and predators in blue. In this sort of model, the prey curve always lead the predator curve.
Critical points occur when 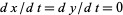 , so
, so
The sole stationary point is therefore located at 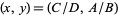 .
.
REFERENCES:
Boyce, W. E. and DiPrima, R. C. Elementary Differential Equations and Boundary Value Problems, 5th ed. New York: Wiley, p. 494, 1992.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 135, 1997.
 الاكثر قراءة في معادلات تفاضلية
الاكثر قراءة في معادلات تفاضلية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


