


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-6-2018
Date: 5-7-2018
Date: 11-6-2018
|
The Laguerre differential equation is given by
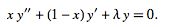 |
(1) |
Equation (1) is a special case of the more general associated Laguerre differential equation, defined by
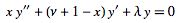 |
(2) |
where 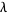 and
and  are real numbers (Iyanaga and Kawada 1980, p. 1481; Zwillinger 1997, p. 124) with
are real numbers (Iyanaga and Kawada 1980, p. 1481; Zwillinger 1997, p. 124) with 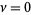 .
.
The general solution to the associated equation (2) is
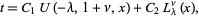 |
(3) |
where 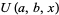 is a confluent hypergeometric function of the first kind and
is a confluent hypergeometric function of the first kind and 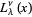 is a generalized Laguerre polynomial.
is a generalized Laguerre polynomial.
Note that in the special case 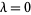 , the associated Laguerre differential equation is of the form
, the associated Laguerre differential equation is of the form
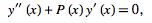 |
(4) |
so the solution can be found using an integrating factor
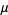 |
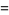 |
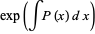 |
(5) |
 |
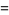 |
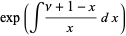 |
(6) |
 |
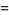 |
![exp[(nu+1)lnx-x]](http://mathworld.wolfram.com/images/equations/LaguerreDifferentialEquation/Inline15.gif) |
(7) |
 |
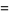 |
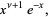 |
(8) |
as
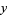 |
 |
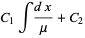 |
(9) |
 |
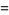 |
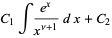 |
(10) |
 |
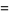 |
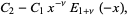 |
(11) |
where 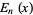 is the En-function.
is the En-function.
The associated Laguerre differential equation has a regular singular point at 0 and an irregular singularity at  . It can be solved using a series expansion,
. It can be solved using a series expansion,
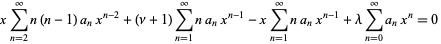 |
(12) |
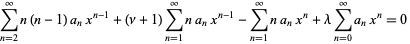 |
(13) |
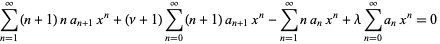 |
(14) |
![[(nu+1)a_1+lambdaa_0]+sum_(n=1)^(infty){[(n+1)n+(nu+1)(n+1)]a_(n+1)-na_n+lambdaa_n}x^n=0](http://mathworld.wolfram.com/images/equations/LaguerreDifferentialEquation/Inline33.gif) |
(15) |
![[(nu+1)a_1+lambdaa_0]+sum_(n=1)^(infty)[(n+1)(n+nu+1)a_(n+1)+(lambda-n)a_n]x^n=0.](http://mathworld.wolfram.com/images/equations/LaguerreDifferentialEquation/Inline34.gif) |
(16) |
This requires
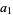 |
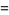 |
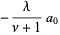 |
(17) |
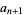 |
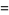 |
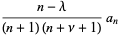 |
(18) |
for 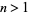 . Therefore,
. Therefore,
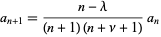 |
(19) |
for 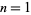 , 2, ..., so
, 2, ..., so
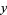 |
 |
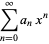 |
(20) |
 |
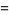 |
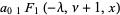 |
(21) |
 |
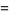 |
![a_0[1-lambda/(nu+1)x-(lambda(1-lambda))/(2(nu+1)(nu+2))x^2-(lambda(1-lambda)(2-lambda))/(2·3(nu+1)(nu+2)(nu+3))x^3+...].](http://mathworld.wolfram.com/images/equations/LaguerreDifferentialEquation/Inline51.gif) |
(22) |
If 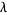 is a nonnegative integer, then the series terminates and the solution is given by
is a nonnegative integer, then the series terminates and the solution is given by
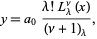 |
(23) |
where 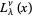 is an associated Laguerre polynomial and
is an associated Laguerre polynomial and 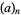 is a Pochhammer symbol. In the special case
is a Pochhammer symbol. In the special case 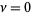 , the associated Laguerre polynomial collapses to a usual Laguerre polynomial and the solution collapses to
, the associated Laguerre polynomial collapses to a usual Laguerre polynomial and the solution collapses to
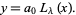 |
(24) |
REFERENCES:
Iyanaga, S. and Kawada, Y. (Eds.). Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1481, 1980.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 120, 1997.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|