Chain Rule

If 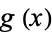 is differentiable at the point  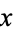and 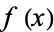 is differentiable at the point 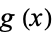, then  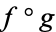is differentiable at 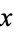. Furthermore, let  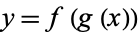and 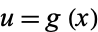, then

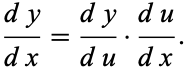(1)

There are a number of related results that also go under the name of "chain rules." For example, if 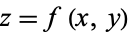, , 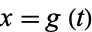and 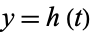, then

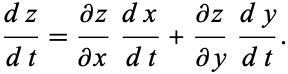(2)

The "general" chain rule applies to two sets of functions

			(3)
			(4)
			(5)

and

			(6)
			(7)
			(8)

Defining the 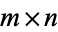 Jacobi rotation matrix by

(9)

and similarly for 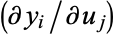 and 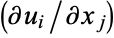, then gives

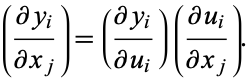(10)

In differential form, this becomes

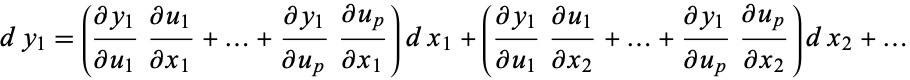(11)

(Kaplan 1984).

REFERENCES:

Anton, H. "The Chain Rule" and "Proof of the Chain Rule." §3.5 and AIII in Calculus with Analytic Geometry, 2nd ed. New York: Wiley, pp. 165-171 and A44-A46, 1999.

Apostol, T. M. "The Chain Rule for Differentiating Composite Functions" and "Applications of the Chain Rule. Related Rates and Implicit Differentiation." §4.10-4.11 in Calculus, 2nd ed., Vol. 1: One-Variable Calculus, with an Introduction to Linear Algebra. Waltham, MA: Blaisdell, pp. 174-179, 1967.

Kaplan, W. "Derivatives and Differentials of Composite Functions" and "The General Chain Rule." §2.8 and 2.9 in Advanced Calculus, 3rd ed. Reading, MA: Addison-Wesley, pp. 101-105 and 106-110, 1984.