Continuity-Dirichlet Function
المؤلف:
Ballone, F. A.
المصدر:
"On Volterra Spaces." Masters thesis, Youngstown State University, Jun. 2010.
الجزء والصفحة:
...
27-4-2018
2492
Continuity-Dirichlet Function
Let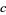 
and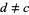 
be real numbers (usually taken as 
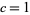and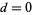 
). The Dirichlet function is defined by
![D(x)=<span style=]() {c for x rational; d for x irrational " class="numberedequation" src="http://mathworld.wolfram.com/images/equations/DirichletFunction/NumberedEquation1.gif" style="border:0px none; height:41px; width:161px" /> |
(1)
|
and is discontinuous everywhere. The Dirichlet function can be written analytically as
 |
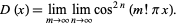(2)
|
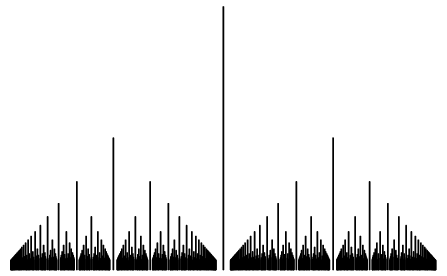
Because the Dirichlet function cannot be plotted without producing a solid blend of lines, a modified version, sometimes itself known as the Dirichlet function (Bruckner et al. 2008), Thomae function (Beanland et al. 2009), or small Riemann function (Ballone 2010, p. 11), can be defined as
![D_M(x)=<span style=]() {0 for x irrational; 1/b for x=a/b a reduced fraction " class="numberedequation" src="http://mathworld.wolfram.com/images/equations/DirichletFunction/NumberedEquation3.gif" style="border:0px none; height:41px; width:275px" /> |
(3)
|
(Dixon 1991), illustrated above. This function is continuous at irrational 
and discontinuous at rational 
(although a small interval around an irrational point 
contains infinitely many rational points, these rationals will have very large denominators). When viewed from a corner along the line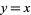 
in normal perspective, a quadrant of Euclid's orchardturns into the modified Dirichlet function (Gosper).
REFERENCES:
Ballone, F. A. "On Volterra Spaces." Masters thesis, Youngstown State University, Jun. 2010.
Beanland, K.; Roberts, J. W.; and Stevenson, C. "Modifications of Thomae's Function and Differentiability." Amer. Math. Monthly116, 531-535, 2009.
Bruckner, A; Bruckner, J.; and Thomson, B. Elementary Real Analysis, 2nd ed.. Upper Saddle River, NJ: Prentice Hall, 2008.
Dixon, R. Mathographics. New York: Dover, pp. 177 and 184-186, 1991.
Tall, D. "The Gradient of a Graph." Math. Teaching 111, 48-52, 1985.
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, pp. 32-33, 2004. http://www.mathematicaguidebooks.org/.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
