
Continuity-Bounded Variation
 المؤلف:
Todd Rowland
المؤلف:
Todd Rowland
 المصدر:
Todd Rowland
المصدر:
Todd Rowland
 الجزء والصفحة:
...
الجزء والصفحة:
...
 25-4-2018
25-4-2018
 2365
2365
Continuity-Bounded Variation
A function 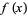 is said to have bounded variation if, over the closed interval
is said to have bounded variation if, over the closed interval ![x in [a,b]](http://mathworld.wolfram.com/images/equations/BoundedVariation/Inline2.gif) , there exists an
, there exists an  such that
such that
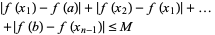 |
(1)
|
for all 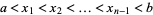 .
.
The space of functions of bounded variation is denoted "BV," and has the seminorm
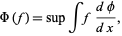 |
(2)
|
where 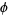 ranges over all compactly supported functions bounded by
ranges over all compactly supported functions bounded by 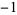 and 1. The seminorm is equal to the supremum over all sums above, and is also equal to
and 1. The seminorm is equal to the supremum over all sums above, and is also equal to 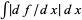 (when this expression makes sense).
(when this expression makes sense).
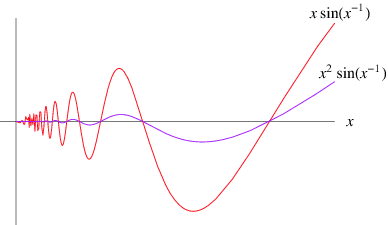
On the interval ![[0,1]](http://mathworld.wolfram.com/images/equations/BoundedVariation/Inline8.gif) , the function
, the function 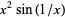 (purple) is of bounded variation, but
(purple) is of bounded variation, but 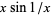 (red) is not. More generally, a function
(red) is not. More generally, a function 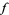 is locally of bounded variation in a domain
is locally of bounded variation in a domain 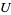 if
if 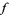 is locally integrable,
is locally integrable, 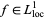 , and for all open subsets
, and for all open subsets 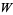 , with compact closure in
, with compact closure in 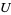 , and all smooth vector fields
, and all smooth vector fields 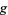 compactly supported in
compactly supported in 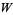 ,
,
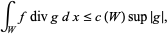 |
(3)
|
div denotes divergence and 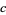 is a constant which only depends on the choice of
is a constant which only depends on the choice of 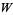 and
and 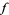 .
.
Such functions form the space 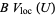 . They may not be differentiable, but by the Riesz representation theorem, the derivative of a
. They may not be differentiable, but by the Riesz representation theorem, the derivative of a 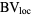 -function
-function 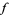 is a regular Borel measure
is a regular Borel measure 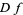 . Functions of bounded variation also satisfy a compactness theorem.
. Functions of bounded variation also satisfy a compactness theorem.
Given a sequence 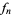 of functions in
of functions in 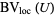 , such that
, such that
![sup_(n)[||f_n||_(L^1(W))+int_W|Df_n|dx]<infty,](http://mathworld.wolfram.com/images/equations/BoundedVariation/NumberedEquation4.gif) |
(4)
|
that is the total variation of the functions is bounded, in any compactly supported open subset 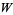 , there is a subsequence
, there is a subsequence 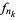 which converges to a function
which converges to a function 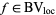 in the topology of
in the topology of 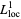 . Moreover, the limit satisfies
. Moreover, the limit satisfies
 |
(5)
|
They also satisfy a version of Poincaré's lemma.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


