
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
التعالق الثلاثي
المؤلف:
أمير أكزيل
المصدر:
التعالق اكبر لغز في الفيزياء
الجزء والصفحة:
ص 195
15-6-2016
3522
التعالق الثلاثي
قال أينشتين إذا كانت ميكانيكا الكم صحيحة فلابد أنه عالم مجنون. وكان أينشتين علي صواب، فالعالم مجنون. دانيال جرينبرجر
ليس لعناصر أينشتين عن الواقع وجود، لا يمكن تقديم تفسير للرقص البديع بين ثلاثة جسيمات من خلال عالم حقيقي موضوعيا . فالجسيمات ببساطة لا تفعل ما تفعله بسبب ما هي عليه، إنما بسبب سحر الكوانتم. مايكل هورن
ميكانيكا الكم هي أشد اكتشافات الإنسان غرابة، لكنها أيضا أكثرها جمالا . وجمال الرياضيات التي تقف داعمة لنظرية الكم تعني أننا اكتشفنا شيئا بالغ الدلالة. أنطون زايلنجر
حين تركنا مؤخرا مايك هورن كان يستمتع بثمار نجاح عمله مع أبنر شيموني، وجون كلاوزر، وريتشارد هولت (CHSH) وبالتفسير الفعلي للتعالق من خلال تجربة تختبر متباينة جون بل، أسفرت عن نتائج تدعم ميكانيكا الكم، وأجراها كلاوزر وفريدمان. علي أن نجاح (CHSH) والتفسيرات التجريبية المصاحبة لها لقيت اهتماما واسع النطاق في الأدبيات الفيزيائية وبثت الجديد في العلم. ونشرت مقالات تفسيرية في عدة مجلات تتناول الاكتشافات الجديدة، وأجريت تجارب جديدة جددت الاهتمام حول أسس العالم العجيب للكوانتم.
وعقب ذلك مباشرة، اشترك كلاوزر، وشيموني، وهورن، مع الرجل الذي استهل العملية جميعها : جون بل. وشرع الرجال الأربعة في اتصالات مسهبة، ظهر بعضها في أوراق بحثية، استهدفت الرد علي التساؤلات ومناقشة الأفكار المطروحة من هنا وهناك. وأسفر هذا الاتصال المثمر عن نتيجة مؤداها أن فرضية جون بل تقوم علي افتراضات أقل تقييدا ، كما أنها تحسن فهمنا لظاهرة التعالق المذهلة.
وكان مايك هورن قد التحق عام 1975 بمجموعة بحثية يرأسها كليف شل Cliff Shull من M.l.T ، قامت بإجراء تجارب علي النيوترونات الناتجة في المفاعل النووي في بكامبردج. وأمضي مايك عشر سنوات في المفاعل، يجري التجارب علي تداخل جسيم وحيد مع النيوترونات. والتقي أيضا مع اثنين من الفيزيائيين سيغيران مجري حياته العلمية، والذي سيثمر عملهما المشترك معه عن قفزة عملاقة في فهمنا للتعالق. وهذان العالمان هما دانيال جرينبرجر وأنطون زايلنجر. وسيكتب الثلاثة ورقة مبدعة تقول إنه يمكن حدوث التعالق بين ثلاثة جسيمات، وسوف يقضون السنوات في دراسة خواص هذا التعالق الثلاثي. وبعد ذلك بعدة سنوات، حينما سألتهم عما إذا كانوا ثلاثتهم علي نحو ما قد "تعالقوا" معا، شأن ثلاثيات الجسيمات التي قاموا بدراستها . رد أنطون زايلنجر علي الفور: "نعم، في الواقع كنا قريبين جدا حتي إنه ما يكاد أحدنا يفتح فمه ليقول شيئا ما، إلا ويكمل الاثنان الآخران العبارة التي علي لسانه".. وثمة سبب وجيه وراء انتقال مايكل هورن من دراساته علي تداخل اثنين من الفوتونات إلي أبحاثه علي تداخل فوتون واحد. فبمجرد الانتهاء من عمل؟؟ الذي ساعد في تأسيس التعالق بوصفه مبدأ أساسيا في أصول ميكانيكا الكم، قرر مايك دراسة قضايا أخري خاصة بجذور هذه الأصول. كان يعرف جيدا تاريخ تطور أفكار نظرية الكم مع تطور أسس هذا الفرع من المعرفة. وكان يعلم أنه عندما أجري يانج تجربته العجيبة باستخدام الضوء في القرن الثامن عشر واكتشف نموذج التداخل الذي ما يزال محيرا لنا حتي يومنا هذا؛ كان الضوء (وغيره من الإشعاعات الكهرومغناطيسية) هو الـ "موجات الميكروسكوبية الوحيدة المعروفة أنذآك. وبطبيعة الحال، حينئذ، وفي عام1905، طرح أينشتين فكرة الفوتون باعتباره حلا للتأثير الكهروضوئي، موضحا أن الضوء ليس فحسب موجة لكنه تيار من الجسيمات أيضا. كما كان مايك يعلم في عام ١٩٢٤ ، أن دي برولي "اخمن أن الجسيمات هي أيضا موجات"، حسب فكرة مايك، إلا أنه "لم يستطع أي شخص في ذلك الحين إجراء تجربة الشق المزدوج باستخدام الإلكترونات رغم التأكيد الصريح من أن الطبيعة الموجية التي اقترحها دي برولي سرعان ما ثبتت نتيجة انحراف الإلكترونات خلال البلورات". وبعد ربع قرن، وفي خمسينيات القرن العشرين، أجري بالفعل الفيزيائي الألماني مولنشتد Moellenstedt وزملاؤه هذه التجربة. وأوضحوا أن هذه الجسيمات، أي الإلكترونات، تبدي الطبيعة الموجية نفسها من خلال نموذج التداخل علي حائل بمجرد نفاذها من جهاز يانج القديم ذي الشق المزدوج.
ومن ثم، وفي منتصف سبعينيات القرن العشرين، أجري هيلموت روش Helmut Rauch في فيينا ، وأعقبه سام ويرنر Sam Werner في ميسوري - كل منهما علي نحو منفصل - تجربة شق مزدوج بشكر أساسي باستخدام النيوترونات. وهذه الأجسام الكمية ذات كتل كبيرة تبدي نماذج التداخل نفسها التي جعلناها ملازمة للموجات وهي تنفذ من جهاز تجربة الشق المزدوج. واستخدم الفريقان، في فيينا وميسوري، كلاهما النيوترونات الحرارية: وهي نيوترونات تنتج عن تفاعلات تحدث داخل مفاعل نووي . وتسير هذه النيوترونات بسرعات بطيئة ("بطئ" مقارنة بسرعة الضوء) تبلغ نحو ألف متر في الثانية، وتبعا لمعادلة دي برولي، تكون أطوال موجاتها المصاحبة عدة أنجسترومات. وهذه التجارب التي كانت تنطوي علي تحديات هائلة غدت الآن ممكنة بفضل التكنولوجيا الجديدة لأشباه الموصلات، التي جعلتها بلورات السليكون النقية ميسورة لي حد كبير. وكان العلماء يستخدمون قطع سيليكون بحجم كف اليد لإنشاء مقاييس التداخل لمواجهة النيوترونات الحرارية القادمة من المفاعل النووي. ونظرا لتفاعل النيوترونات مع الشبكة البلورية، كان شعاع النيوترونات في البداية ينقسم بالانحراف علي أحد أوجه البلورة، ثم تستخدم الأوجه الأخرى لإعادته إلي وجهته وفي النهاية تتحد الأشعة لتنتج نموذج التداخل.
كان مايك شديد الاهتمام بهذه التجارب، التي كان قد تم إجراؤها في التو. وكان يعلم أن كليف شل - أحد رواد بحوث النيوترونات في أربعينيات القرن العشرين، (وسينال جائزة نوبل عام ١٩٩٤) - لديه معمل في مفاعل M.l.T وأن عمله هناك يتمثل في إجراء التجارب علي النيوترونات الحرارية. كان مايك في ذلك الحين يشغل منصبا في تدريس الفيزياء في كلية Stonehill ، ولم يكن يوجد مفاعل في ستونهل كما لا يوجد بها فيزيائي معروف يشرف علي توجيه الأبحاث الجديدة المثيرة. ولذلك، وفي أحد أيام عام 1975 ، شق مايك طريقه إلي معمل كليف شل في M.l.T ، وقدم نفسه. وذكر لشل عمله في التعالق مع أبنر شيموني وجون كلاوزر، واهتمامه بتجارب تداخل النيوترون، ثم سأل: "أيمكنني أن أؤدي دورا؟".
وكان رد شل وهو يشير إلي أحد المكاتب في جانب من المعمل: ´´خذ هذا المكتب هناك، ومن ذلك اليوم فصاعدا، طوال عشر سنوات، منذ عام1975 حتي 1985، في كل صيف، وكل اجازة لأعياد الميلاد، وكل أيام الثلاثاء (حيث لا يعمل بالتدريس)، كان مايك هورن يمضي أوقاته في معمل شل بمفاعل M.I.T النووي يواصل العمل علي حيود النيوترون. ووجد تجربتين فقط جذبتا اهتمامه بشكل خاص كانتا قد أجريتا بالفعل باستخدام النيوترونات في فيينا وميسوري، وكانت مجموعة كليف شل قد أجرت تجارب أخري كثيرة من هذا النوع في M.I.T.
وتوضح التجربة - التي أجراها سام ويرنر ومعاونوه في جامعة ميسوري عام 1975 - أن تداخل النيوترون بتجربة الشق المزدوج يتأثر تأثرا مباشرا بالجاذبية وهو الأمر الذي لم يكن معلوما من قبل. إذ لم يتضح قط من قبل أي تأثير للجاذبية في التداخل في ميكانيكا الكم. كانت تجربة ميسوري بارعة وفي الوقت نفسه تنطوي علي بساطة المفهوم، وبالتالي تقدم تفسيرا لجوهر العديد من هذه التجارب الكمية.
كان قد تم ترتيب المسارين في مقياس التداخل في شكل ماسة Diamond وبمجرد دخول النيوترون إلي الماسة تنقسم موجته الكمية عند المدخل، ويتجه نصف الموجة يسارا ، والنصف الآخر إلي اليمين. وفي الطرف الآخر للماسة، حيث يعود نصفا الموجة للاتحاد والاستثارة، كان يوجد إما قمة أو قاع حسب الشدة - كما يحدث تماما علي الشاشة في تجربة يانج الكلاسيكية، فيما غدا أن هذا يحدث هنا في نقطة واحدة وليس في نقاط متصلة علي شاشة. وسجل العلماء أنهم وجدوا إما قمة أو قاعا . وبعد ذلك، وبإدارة بلورة السيليكون، أداروا الماسة بمقدار 90 درجة حتي تصبح رأسية وليست أفقية. ولاحظوا في هذه الحالة تغيرا في الشكل. وكان السبب في هذا أن موجتي النيوترون تأثرتا بالجاذبية، إذ كانت إحداهما أعلي من الاخرى، ويسير النيوترون الأعلى بسرعة أقل. وأدي هذا إلي تغير في طول موجة دي برولي علي امتداد أحد المسارين مقارنة بالآخر، وبالتالي حدثت إزاحة لنموذج التداخل. والشكل التالي يوضح هذه التجربة.
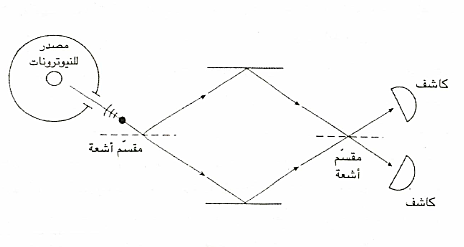
ثمة تجربة أخري أجراها هيلموت روش وزملاؤه في فيينا عام 1975، وكذلك مجموعة ميسوري في تلك السنة، وهي تجربة 2π - 4πباستخدام النيوترونات. واكتشف فريق فيينا الذي يقوده روش باستخدام مقياس التداخل النيوتروني خاصية مبهرة للنيوترونات. فقد تم استخدام مجال مغناطيسي لتدوير النيوترون في أحد مسارات مقياس التداخل بمقدار 360 درجة (2π )، وفي حين أن الجسيمات التي يحدث لها حركة دورانية كاملة المسماة البوزونات Boson، عندما تجري لها دورة مماثلة، تعود إلي حالتها الأصلية (ذلك لأنها هكذا تدور دورة كاملة)، لكن الأمر نفسه لا يحدث للنيوترون بعد الدوران حول زاوية قيمتها 360 ، أي دورة كاملة، ويتضح أن النيوترونات حدث لها تغير جيبي (أي جيب الزاوية - المترجم) الذي يمكن ملاحظته من خلال ظاهرة التداخل. وعندما يؤدي المجال المغناطيسي لدوران النيوترونات مرة أخري حول الدائرة (أي بمقدار4π )، فإن النيوترونات تعود إلي حالتها الأصلية.
وفي بوسطن، تحدث أبنر شيموني مع مايك هورن أثناء الفترة نفسها حول إجراء هذا النوع من التجارب باستخدام النيوترونات، بهدف البرهنة علي ما هو معروف نظريا بشأن خاصية (2π - 4π) ، النيوترونية دون أن يكونا علي علم بأن روش وتلامذته في فيينا قد أجروا بالفعل التجربة نفسها . وكتب مايك وأبنر ورقتهما وأرسلاها إلي مجلة للفيزياء. لكنهما سرعان ما اكتشفا أن مجموعة فيينا قد أجرت بالفعل الأمر نفسه وأنهما نفذا التجربة. وكان بين طلاب روش في فيينا أنطون زايلنجر.
ولد أنطون زيلنجر في مايو 1945، في ريد/نكريس بالنمسا . وبين عامي 1963 ، ١٩٧١ درس الفيزياء والرياضيات بجامعة فيينا وحصل علي شهادة الدكتوراه في الفيزياء من الجامعة عام ١٩٧١، وكان موضوعها عن "اللا استقطاب النيوتروني في بلورات الديسبروزيوم المفردة"، والتي كتبها تحت إشراف البروفيسور روش. وفي عام ١٩٧٩ أدي بحثه التأهيلي Habilitation ، حول النيوترون وفيزياء الجوامد solid state في الجامعة الفنيةtechnical بفيينا . وبين عامي ١٩٧٢ ، ١٩٨١ عمل مساعدا جامعيا في معهد البحوث الذرية بفيينا، ومرة أخري كان يعمل مع روش.
توجد في صقلية مدينة صغيرة رائعة تعود إلي القرون الوسطي تسمىErice ، وليس الفيزيائيون بغرباء عن الجمال والطبيعة لذلك وقعوا في غرام هذه البلدة، المقفرة التي تلفها جبال جزيرة صقلية، ونظموا سلسلة من المؤتمرات السنوية بها، شدت إليها الفيزيائيين من كل أنحاء المعمورة. وفي عام ١٩٧٢ ، تم تخصيص المؤتمر المنعقد بها لأصول ميكانيكا الكم، بحيث يشمل دراسات عن متباينات جون بل و التعالق، وحينما تلقي روش إعلانا بالاجتماع سأل أنطون زايلنجر: "لماذا لا تذهب إلى الاجتماع؟" نحن لا نعرف الكثير عن أبحاث جون بل، لكن بمقدورنا أن نتعلم، وربما نتمكن ذات يوم من إجراء مثل هذه التجارب المثيرة، وكما سمعت فسوف يشارك الباحثون المشتغلون في التعالق، بمن فيهم مجموعة فيينا ... هيا اذهب وتعلم قدر استطاعتك. كان أنطون سعيدا بموافقته، وحزم أمتعته للذهاب إلي صقلية.
وفي الوقت نفسه، في بوسطن، كان أبنر، ومايك، وفرانك بيبكين من هارفارد يعدون حقائبهم أيضا، استعدادا للرحيل إلي صقلية، ومعهم مجموعة أوراق حول أبحاثهم في التعالق ليعرضوها في الاجتماع. وكانت ورقة مايك هورن المخصصة للاجتماع تتضمن عمله مع جون كلاوزر الذي دام عدة سنوات ، وكذلك استكمالا لفرضية جون بل التي تتعلق بالأوضاع الاحتماليةprobabilistic settings. وفي صقلية، التقي فيزيائيو بوسطن مع أنطون زايلنجر للمرة الأولي. وقال مايك هورن: ´´اتفقنا معا مباشرة وأضاف: ´´كان أنطون بالغ الاهتمام. وحاول أن يتعلم مني كل ما يستطيع عن فرضية جون بل، كان مفتونا بالتعالق.
وبعد العودة إلي معمل كليف شل حيث المفاعل النووي في؟؟، وفي أحد الأيام توجه كليف إلي مايك متسائلا: هل تعرف شخصا اسمه أنطون زايلنجر؟ وهو يشير إلي خطاب في يده: لقد كتب طلبا يبدي رغبته في الحضور إلي هنا، وذكر اسمك في خطابه. وأجاب مايك: "أوه، بالتأكيد. هذا شيء رائع. وأضاف: إنه فيزيائي مبهر.. شديد الاهتمام بأصول ميكانيكا الكم".
وانضم أنطون زايلنجر إلي فريق العمل في M.l.T في العام الدراسي77/1978 كزميل لما بعد الدكتوراه، مدعوما بمنحة فولبرايت للزمالة Fulbright ، وعلي مدي السنوات العشر التالية، وحينما أصبح بالفعل أستاذا في فيينا، كان يأتي إلي كامبردج في مهام محددة كثيرة، تدوم كل واحدة منها عدة شهور. وكان ينهمك في العمل ليقوم بالنوع نفسه من أبحاث حيود النيوترونات التي كان يؤديها وهو طالب مع روش في فيينا ، وأمكن أن يشارك مايك هورن في كتابة عدد كبير من أوراق البحث طوال سنوات، ومعهما كليف شل والطلاب العاملين معهم بالمعمل في ذلك الحين، وكان الطلاب يتغيرون من سنة إلي أخري. وظل يعمل علي هذا المنوال حتي أحيل كيف شل إلي التقاعد عام ١٩٨٧ .
وأثناء تناول الساندوتشات، في أوقات الراحة بالمعمل، ربما يجلس أنطون ومايك معا يناقشان تداخل جسيمين، وهو العمل القديم لمايك مع أبنر وجون وديك هولت. إلا أن عملهما الحالي كان يتضمن دراسات التداخل للنيترون المفرد. فقد باتت تجارب الجسيمين، وأفكار فرضية جون بل أنذآك مجرد هواية عاطفية، أحد الاهتمامات خارج عملهما اليومي. وفي استعادة مايك هورن لذكريات هذه الفترة يقول: "كنا نجلس هناك، لتناول غدائنا وكنت أزوده بالمعلومات عن فرضية جون بل والمتغيرات الخافية الموضعية، وكيف أنها لا تتفق مع ميكانيكا الكم"، ويضيف: "دائما ما كان يصغي بانتباه، راغبا في سماع المزيد والمزيد".
ولد دانيال جرينبرجر في the Bronx عام ١٩٣٣. والتحق بالمدرسة الثانوية للعلوم في برونكس وكان في الصف نفسه مع ميريام ساراشيك Myriam Sarachik (الرئيس المنتخب للجمعية الفيزيائية الأمريكية، وهي الآن زميل لدانيال في CCNY ، والفيزيائيين الحاصلين علي جائزة نوبل شيلدون (شيلي) وجلاشو Glashow وستيفن واينبرج. وعقب ذلك درس داني (تصغير دانيال) الفيزياء في Steven Weinberg وتخرج عام 1954. ثم ارتحل إلي جامعة إلينوي Illinois لإجراء بحوثه في الدكتوراه في مجال فيزياء الطاقة العالية مع فرانسيس لاو. Francis Low. وبعد رحيل لاو ليتولى منصبا فيM.I.T، خلفا جرينبرجر، وكتب أطروحته في M.l.T للحصول علي الدكتوراه في الفيزياء. وهناك درس الفيزياء الرياضية، بما فيها الطرق الجبرية باستخدام السيمتريات، التي أصبحت شائعة حاليا في الفيزياء النظرية الحديثة، وفي مطلع ستينيات القرن العشرين، انضم إلي جيفري شيو Jeffrey Chew في جامعة كاليفورنيا ببيركلي، ليعمل في زمالة ما بعد الدكتوراه في فيزياء الطاقة العالية. وتناهي إلي سمعه بعد ذلك أن سيتي كولدج City College في نيويورك افتتحت مدرسة للخريجين وتتضمن مقررات في الفيزياء. لذلك ذهب إلي هناك في عام 1963وأصبح يعمل بتلك الكلية منذ ذلك الوقت وحتي الان.
وظل داني علي الدوام مفتونا بنظرية الكم. وفي دفاعه عنها يؤكد أن ميكانيكا الكم ليست مجرد نظرية تنضم إلي الفيزياء الكلاسيكية، عندما يزداد حجم الأجسام موضع الدراسة، بل إنها نظرية مستقلة تتمتع بثراء هائل لا يتبدى لنا مباشرة. ويشبه جرينبرجر نظرية الكم بجزر هاواي. وحسب مقاربتنا لهذه الجزر، فلا نري منها سوي الجزء المرتفع عن سطح الماء: الجبال، والشواطئ. أما ما تحت السطح فثمة أجزاء هائلة خافية من هذه الجزر، تمتد إلي أعماق المحيط الباسيفيكي Pacific Ocean وكمثال لتوضيح أن ميكانيكا الكم ليست مجرد امتداد للفيزياء الكلاسيكية، بل إنها تملك هذا البعد الخفي، يطرح دانيال جرينبرجر فكرة دوران الأجسام الفيزيائية. ويذكرنا بأن كمية الحركة الزاوية وهي أحد عناصر الفيزياء الكلاسيكية لها ما يناظرها في ميكانيكا الكم. لكن الحركة الدورانية Spin فلا توجد فقط إلا للأجسام الميكروسكوبية. وهي من مكونات عالم الكم وليس لها ما يناظرها في الفيزياء الكلاسيكية.
وكان جرينبرجر مهتما بالتفاعل بين النظرية النسبية وميكانيكا الكم. وخصوصا ، كان يريد اختبار مدي صحة مبدأ أينشتين المهم عن تسامي، القصور الذاتي للكتل وخضوعها للجاذبية الأرضية علي مستوي ميكانيكا الكم. ولكي يقوم بذلك، تأكد لديه أنه يحتاج إلي دراسة الأجسام الكمية التي تتأثر أيضا بالجاذبية الأرضية. وكان يعلم أن من هذه الأجسام النيوترون. ودائما ما يتطلع الفيزيائيون لمعرفة الصلة بين النظرية النسبية العامة، وهي النظرية الحديثة للجاذبية الأرضية، وعالم الكوانتم. والنيوترونات من العناصر الكمية ذلك لأنها صغيرة الحجم، إلا أنها تتأثر أيضا بالجاذبية الأرضية. لذلك، ربما يمكن التوصل للصلات بين هاتين النظريتين بدراسة النيوترونات.
وأجرى جرينبرجر اتصالا بالعلماء العاملين في مفاعل أبحاث Brookhaven National (المعمل القومي في بروكهافن) في لونج أيلاند Long Island من أجل إجراء بحوث خاصة بالنيوترون، لكنهم أبلغوه بأنه لم يسبق لهم القيام بدراسات علي التداخل باستخدام النيوترونات. ومع ذلك، اكتشف أن كيف شل في M.l.T سبق له إجراء مثل هذه البحوث، وفي عام 1970 سافر داني إلي كامبردج للقائه. وعقب ذلك بخمس سنوات طالع مقالا كتبه كل من كوليلا Colella ، وأوفر هاوزر Over Hauser ، وويرنر حول تأثير أهارونوف - بوهم، وأجري اتصالا مع أوفر هاوزر وتبادل معه الرأي حول هذا التأثير. وأيقن داني أن ثمة مظهرا يحتاج إلي كشف الغطاء عنه. وفيما بعد نشر ورقة حول هذا التأثير في مجلة ريفيو أوف مودرن فيزيكس Review of Modern Physics . وفي عام ١٩٧٨، تم تنظيم مؤتمر لبحث هذه الموضوعات الفيزيائية بالمفاعل النووي الكبير في جرينوبل بفرنسا . ولم يستطع أوفر هاوزر - الذي نلقي دعوة لحضور المؤتمر الذهاب إليه وطلب من جرينبرجر - إن كان لا يمانع، الذهاب بدلا منه.
وفي جرينوبل، التقي داني مع أنطون زايلنجر، الذي كان يعمل أنذآك بمفاعل جرينوبل بمعهد Grenoble ، باحثا زائرا لبعض الوقت. كما تقابل مع مايك هورن، وكان مثل داني يحضر المؤتمر. ونظرا لأن الثلاثة - جرينبرجر وهورن وزايلنجر - كانوا جميعا مهتمين بالموضوع نفسه، تأسست رابطة بينهم. ويتذكر جرينبرجر: ´´لقد غير هذا الاجتماع حياتي. ويضيف: "اتفقنا نحن الثلاثة حقيقة معا". ومن جرينوبل عاد أنطون إلي النمسا ليواصل بحوثه هناك، وعقب عودته إلى M.I.T، غمرته السعادة حين وجد أن داني جرينبرجر قد انضم أيضا إلى فريق M.I.T ، في زيارة قصيرة. إلا أن الزيارة سوف تتكرر مرات ومرات مجددا لسنوات عديدة. حتي إحالة كليف شل للمعاش في عام ١٩٨٧ - وهو ما أتاح للعلماء الثلاثة العمل معا عن قرب. وحتي بعد إقالة كيف، ومن خلال منحة N.S.F لهم مع هيرب برنشتين Herb Bernstein من هامبشير كولدج أتيح لهم مواصلة بحوثهم.
استمر ذهاب أنطون إلي M.I.T ليمكث بها عدة شهور، وأحيانا سنوات في كل مرة، بينما يأتي داني في زيارات خاطفة تستمر عدة أسابيع في المرة الواحدة. وكان الاستثناء الوحيد بقاء داني لفترة طويلة عام 1980، حيث حصل علي عطلات أيام السبت (السنة السبتية). وسرعان ما أضحي العلماء الثلاثة مجموعة متألفة متماسكة داخل جماعة العلماء الاكبر العاملة في مفاعل M.I.T ، وكانوا ينفقون الساعات الطوال فارج المعمل يتحدثون عن التعالق، وهو الموضوع الذي شغل جانبا كبيرا من اهتمامهم. وفي داخل المعمل كانوا يعملون حصريا علي تداخل جسيم واحد (النيوترون)، وتركزت الكثير من مناقشاتهم خارج المعمل علي التداخل الناجم عن جسيمين وكذلك عن فرضية جون بل الساحرة.
وكان التعالق كاملا بين الفيزيائيين الثلاثة. فقد لاحظ داني ومايك في اللحظة نفسها بعض الأمور الرياضية الغامضة فيما يتعلق بتأثير أهارونوف - بوهم الشهير الذي نشر في خمسينيات القرن العشرين، وعلي نحو مستقل بحث كل منهما المسالة. وسجل داني جرينبرجر نتائجه ونشرها في إحدى المجلات. وكثيرا ما توصل أنطون وداني إلي أفكار بينها روابط وثيقة حول الفيزياء، والأمر نفسه قد يحدث بين مايك وأنطون، اللذين استمرا لعشر سنوات يكتبان أوراقا مشتركة حول أبحاثهما المتعلقة بتداخل جسيم واحد اعتمادا علي عملهما في معمل شل. وفي عام 1980، أصدر مايك وأنطون ورقة مشتركة حول التعالق تقترح إجراء تجربة توضح أن الظاهرة تتحقق أيضا بالنسبة لأوضاع جسيمين (إضافة إلي الحركة الدورانية أو الاستقطاب)، كما أنه يمكن تطبيق فرضية جون بل في هذه الحالة.
وذات يوم من عام 1985، وصلت دعوة إلي أنطون ومايك عن مؤتمر ينعقد في فلنده احتفالا بالعيد الخمسين لصدور ورقة أينشتين وبودولسكي وروسين (EPR) والثورة التي أحدثتها في العلم. وقررا أن الذهاب إلي فلنده ينطوي علي فوائد عظيمة، إلا أنهما كانا بحاجة إلي ورقة حول تداخل جسيمين لعرضها بالمؤتمر، فقد كان بحثهما عن الجسيم الواحد غير مناسب. وفي غضون عدة أيام تمكنا من الحصول علي تصميم لماسة مزدوجة لتجربة من نوع جديد لاختبار متباينة جون بل. وهكذا صار لديهما ورقة للمؤتمر. وتمكت الفكرة في إنتاج فوتونات متعالقة يتلوها إجراء تجربة لتداخل هذه الفوتونات، باستخدام ماسة مزدوجة .
والشكل التالي يوضح هذا التصميم
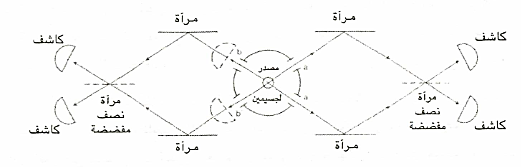
وفي تصميم هذه التجربة، ثمة مصدر من نوع خاص يبث في أن واحد زوجا من الجسيمات A, B، ينطلقان في اتجاهين متضادين. وبالتالي يمكن لهذا الزوج أن يمر إما من الفتحة a أو الفتحة b علي الترتيب، أو من خلال الفتحتين a, 'b'. وبفرض أن الجسيمB تم احتجازه عند أي من فتحتي الكاشفين'b, b. فإذا كان الجسيمB قد استقر عند b إذن يكون الجسيم A قد اتخذ الفتحة a . وبالطريقة نفسها ، إذا استقر الجسيم B عند 'b ، إذن فإننا نعرف أنA قد أخذ الفتحة'a . وبالتالي لكل 100 زوج ينتجه هذا المصدر فإن الكاشفين العلويين سيسجل كل واحد منهما 50 جسيما من نوع "A" بمعني، أنه لا يوجد تداخل لجسيم واحد هنا، ذلك لأنه بالتوصل إلي الجسيمB يمكن اكتشاف المسار الذي اتخذه الجسيم A. وفي واقع الأمر، ليس من الضروري إدخال أجهزة الكشف بالقرب من الفتحتين b ، 'b إذ تكفينا فحسب حقيقة أننا نستطيع تحديد الفتحة التي اتخذها الجسيم B لنلغي تداخل الجسيم الواحد بالنسبة للجسيمA.
ولنتخيل أننا ألغينا الكاشفين عند b ، 'b وأبقينا مراقبة الكاشفين A"" العلويين والكاشفين "B" السفليين مع انبعاث 100 زوج من الجسيمات من المصدر. وتتنبأ ميكانيكا الكم أن كل كاشف سيسجل50 جسيما ، أي لن يكون ثمة تداخل لجسيم واحد لكل من A, B لأننا استطعنا تحديد المسار الذي اتخذه كل جسيم منهما باحتجاز الجسيم الآخر قريبا من المصدر. بيد أن ميكانيكا الكم تتنبأ بمعاملات ارتباط مذهلة بين عدادات القياس. وذا استقر الجسيمB عند الكاشف الأيسر لأسفل، فإن A بالتأكيد يستقر بالكاشف الأيمن لأعلى؛ واذا وجدنا B في الكاشف الأيمن السفلي، لاستقر A في الكاشف الأيسر لأعلى. إذ إن الكاشفين الأيسر السفلي والأيسر العلوي لا يعملان معا، وكذلك لا يعمل معا الكاشفان الأيمن السفلي والأيمن العلوي. ومع ذلك، إذا أزحنا أحد مقسمي الأشعة لمسافة مناسبة يمينا أو يسارا ، تتغير معاملات الارتباط كليا . والآن في حالة عمل الكاشفين في الناحية اليسرى وفي الناحية اليمني بترابط متزامن فإنه لا يعمل الكاشفان الموجودان علي القطر نفسه، لكن لازال معدل العد لكل كاشف ثابتا عند؟، مستقلا عن مواضع جهازي تقسيم الأشعة. ويقول هذا السلوك في ميكانيكا الكم إن كل زوج من الجسيمات ينبعث -خلال الفتحتين 'a، 'b وكذلك خلال الفتحتين a، b، وهذه الحالة الكمية الغامضة تعد مثالا علي تعالق جسيمين).
في أحد الأيام، وقد جلس مايك هورن، وداني جرينبرجر في المطبخ بمنزل الأول، سأله داني: "ما رأيك فيما سيحدث عند تعالق ثلاثة جسيمات؟". كان السؤال، في المقام الأول، ما هي تفاصيل معاملات ارتباط الجسيمات الثلاثة؟ وكان السؤال أيضا : كيف يمكن لورقة EPR أن تتعامل مع ثلاث جسيمات متعالقة؟ ألا يمكن أن توجد أي مصاعب خاصة في محاولة تقديم تقدير واقعي موضعي للتعالق، أو أيكون الخلاف بين ميكانيكا الكم وموضع أينشتين هو بصورة أساسية الخلاف نفسه كما في زوج الجسيمات: بات داني مقتنعا أن هذا كان اتجاها في البحث جديرا باهتمامه خلال عطلته السبتية القادمة. وبعد تفكير في التجارب المحتملة، راح يستعيد في ذاكرته تجهيزات وو - شاكنوف في الانبعاث البوزيتروني، حيث كان يتسبب الجسيمان في إلغاء بعضهما البعض، وعادة ما كان ينبعث فوتونان عاليا الطاقة، لكن، وحسب قوانين الاحتمالات في ميكانيكا الكم، كانت تنبعث ثلاثة فوتونات غالبا بالكيفية نفسها أيضا . وكان هذا تجهيزا لتجربة يمكن الاحتفاظ به في الذهن خلال المشروع البحثي الجديد. وتفكر مايك هورن في سؤال داني، ثم أجاب: "أعتقد أن ذلك سيكون موضوعا عظيما جديرا بالبحث" . وعاد جرينبرجر إلي منزله، مشغول الفكر بالمسالة. وفي غضون الشهور القليلة التالية، كان يتصل بمايك قائلا: "إنني أحصل علي نتائج مهمة لتعالق ثلاثة جسيمات - عندي متباينات تروح وتجيء في كل مكان؟ في اعتقادي أن تعالق ثلاثة جسيمات قد يكون تحديا عظيما لورقة EPR أكثر من تعالق جسيمين". كان مايك مهتما . بيد أنه كان يعلم أن فرضية جون بل وأن التجارب أثبتت فعليا عدم صحة ورقة EPR، وبالتالي ليست هناك حاجة ضاغطة إلي برهان أخر. إلا أن درجة اهتمامه بفيزياء تعالق الجسيمات الثلاثة كانت كافية لمناقشة الوضع مع داني وحثته علي الاستمرار.
وفي عام 1986، حين عاد أنطون إلي فيينا ليواصل العمل مع روش، كوفئ داني بمنحة زمالة فولبرايت، مما أتاح له السفر إلي أوروبا في عام إجازته وقرر أن ينتهز الفرصة لينضم إلي أنطون ويعمل معه في النمسا . وكانت قضية تعالق الجسيمات الثلاثة ما تزال تدور بشدة برأسه إبان سفره عبر الأطلنطي. وحين وصل إلي فيينا ، كانت قد اختمرت لدي داني بالفعل الكثير من الأفكار الجيدة، كان يشعر أنه اقترب من وضع فرضية جون بل بدون متباينات. وفي فيينا ، اقتسم أنطون وداني مكتبا واحدا ، وكان داني يعرض دائما علي أنطون تطورات نتائجه النظرية، وكان الاثنان يتناقشان فيها بالتفصيل. وفي نهاية الأمر، غدا في مواجهة داني جرينبربر وضع ينطوي علي معامل ارتباط كامل بين الجسيمات الثلاثة كافيا لإثبات فرضية جون بل. لم تعد ثمة حاجة إلي ابحث عن معامل ارتباط جزئي بين الفوتونين، مثلما حدث تجريبيا علي يد كلاوزر، وفريدمان، وأسبكت وأخرين. الآن أصبح هناك إثبات فعال علي نحو باهر وحتي أكثر بساطة من الناحية المفاهيمية لفرضية جون بل. وقال داني: "هيا بنا ننشره!" وأضاف أنطور أنه أجري مع مايك بعض العمل المشترك المتصل بالموضوع وينبغي تضمينه في الورقة نفسها . وتباحث الاثنان مع مايك هورن في بوسطن عبر الهاتف، وتقرر العمل في ورقة حول الموضوع.
وفي عام 1988، كان مايك يتصفح عددا من مجلة فيزيكال ريفيو ليترز في معمل شل ولاحظ ورقة كتبها ليونارد ماندل. واحتوت الورقة علي تصميم لتجربة مماثلة تقريبا للتصميم الذي سبق واقترحه هو وأنطون في عرضهما بمؤتمر فلنده. وتمثل الفرق الوحيد أنه في تصميم تجربة تداخل جسيمين لماندل كانت هناك ماسة مطوية بدلا من الماسة المستقيمة كما في الشكل المقترح من هورن - زايلنجر. فير أن ماندل - الذي لم يكن قد شاهد محاضر جلسات مؤتمر فلنده - قد أجرء أيضا التجربة فعليا، واستخدم طريقة التحويل لأدني لإنتاج فوتونات متعالقة. وهكذا ، لم تكن تجربة تداخل جسيمين مجرد تجربة فكرية، بل أصبحت حقيقة واقعة. أكثر من هذا ، غدا في الإمكان الآن إجراء تجارب جون بل مع تعالق شعاع وبدون حركة دورانية أو استقطاب.
ونظرا لأن أنطون ومايك قد اقتصرا علي تقديم افتراضهما عن تداخل جسمين، وعن تجارب جون بل بدون استقطاب في المؤتمرات، ونظرا لأن فهمهما لأسس التعالق بالنسبة إلي التداخل كان مختلفا وأكثر بساطة من ماندل، لذلك قررا تقديم نتائجها إلي الفيزيكال ريفير ليترز لنشرها ، وانضم إليهما أبنر في كتابة الورقة. ولأن الورقة كانت علي نحو أساسي تعليقا علي تجربة ماندل التي تعد اختراقا ، فإن المجلة انتدبت ماندل بنفسه ليفصل في الأمر. وأعقب ذلك فترة طويلة من النشاط والتعاون تواصل فيها بحث تداخل الجسيمين باستخدام التحويل لأدني علي يد فريق بوسطن، وماندل في روشست، وشيه في ميريلاند، وأخرين.
عامين لم يطرأ أي جديد بالنسبة إلي نتائج الحديثة المبهرة حول تداخل الجسيمات الثلاثة. وبعد ذلك، وفي عام ١٩٨٨، نال داني منحة زمالة ألكسندر فون همبولدت Alexander Von Humboldt لإجراء بحث في جارشنج Garching بألمانيا في معهد ماكس بلانك، ليقضي هناك ثمانية أشهر كباحث زائر. وأثناء وجوده هناك اتصل هاتفيا بأنطون في فيينا قائلا: "الأن لدي وقت للكتابة"، وأضاف: "لقد انتهيت من كتابة 70 صفحة. وإن كنت لم أكد أبدأ بعد".. إلا أن الكتابة التقليدية للورقة لم يحدث بها تقدم. فقد قام داني بجولة في أوروبا، يجري أحاديث حول عمله مع أنطون ومايك يتعلق بخواص الجسيمات الثلاثة المتعالقة ومدي الصلة بينها وبين فرضية جون بل وورقة EPR. ومع نهاية صيف ١٩٨٨ ، ذهب داني جرينبرجر إلي مؤتمر Erice بصقلية لذلك العام. وتحدث حول تعالق الجسيمات الثلاثة، وكان من بين المستمعين دافيد ميرمين David Mermin من كورنل وهو فيزيائي متخصص في الكوانتم. ووفقا لما ذكر داني أنه أحس بأن الورقة لم تجذب في الواقع اهتمام ميرمين.
لكن حين عاد داني إلي نيويورك، بدأ يتلقى أوراقا من مجموعات عديدة للفيزيائيين يستخدمون فيها عمله الأصلي مع مايك وأنطون كمرجع. وكان من بين مجموعات الفيزيائيين هذه واحدة يرأسها مايكل ردهيد Michael Redhead من جامعة كامبردج. وزعمت مجموعة ردهيد أنها أجرت تحسينات علي عمل جرينبرجر - هورن - زايلنجر حول تداخل الجسيمات الثلاثة، الذي سبق وقدمه .اني في مؤتمر Erice وفي أماكن أخري بأوروبا . واتصل داني تليفونيا بأنطون ومايك وقال: "لابد أن نفعل شيئا في الحال، الناس حاليا يستخدمون عملنا كمرجع دون أن يتم نشره حتى الآن".
وفي عام ١٩٨٨، تقدم داني بورقة، نشرت في مؤتمر للفيزياء عقد بجامعة جورج فاسون. وفي الوقت نفسه تلقي دافيد ميرمين ورقة ردهيد، التي استخدمت عمل جرينبرجر، وهورن، وزايلنجر مرجعا لها . وفي عموده تحت عنوان "إطار مرجعي Reference Frame في مجلة Physics Today ، كتب ميرمين مقالا عنوانه: أين الخطأ في عناصر الواقع هذه". وكانت مجلة فيزيكس توداي هي المجلة الإخبارية التي تصدرها الجمعية الأمريكية للفيزياء، وبالتالي حققت الورقة انتشارا واسعا ، وأضحي المجتمع الفيزيائي علي علم كامل بالنتائج الجديدة، وراح يستخدمها مرجعيا علي النحو "تعالق GHZ - رغم أن الورقة المشتركة لكل من جرينبرجر، وهورن، وزايلنجر لم تكن قد نشرت بعد. (في كثير من العلوم، فإن الورقة المدرجة ضمن وقائع جلسات أي مؤتمر لا تعتبر بنفس مستوي ورقة منشورة في مجلة مرجعية). وفي الواقع، فإن اثنين من مؤلفي الورقة لم يكونا علي علم بأن ورقة تحمل اسميهما تم تقديمها في مؤتمر، ونشرت ضمن وقائع جلساته. فقد نسي داني أن يخبرهما بهذه الواقعة.
وذات يوم قال أبنر لمايك: "ما هو الشيء الذي برهنت عليه أنت وداني وأنطون؟"، فرد مايك متسائلا: "ما هو هذا الشيء؟، فأعطاه أبنر ورقة دافيد ميرمين. وكان ميرمين في ورقته يشرح أن ميكانيكا الكم تتعارض مع المتغيرات الخافية، وبالتحديد في حالة الجسيمات الثلاثة المتعالقة، وقد نسب بوضوح هذا البرهان الذي قدمه إلي جرينبرجر، وهورن، وزايلنجر. وقبل أن يعرف السبب، تلقي مايك مراسلات من المجتمع الفيزيائي تهنئه علي نجاح ورقة GHZ. وفي25 نوفمبر1990، بعث جون كلاوزر ببطاقة إلي مايك هورن من بيركلي يقول فيها:
"عزيزي مايك:
أيها الثعلب العجوز، ابعث لي بنسخة من GHZ. يبدو أن ميرمين يعتقد أنها مادة فائقة السخونة".
ووصلت بعض التهاني من أناس علي قمة المهنة، بمن فيهم حاصلون علي جائزة نوبل. وسرعان ما أدرك الفيزيائيون الثلاثة أنه من المناسب نشر بحثهم في مجلة مناسبة. ولذلك، وجهوا دعوة إلي أبنر شيموني للانضمام إليهم، نظرا لأنه كان يؤدي عمل جون بل منذ البداية. وفي عام1990، صدرت الورقة ´´فرضية جون بل بدون متباينات´´ تأليف جرينبرجر، هورن، شيموني، وزايلنجر، في المجلة الأمريكية للفيزياء American Journal of Physics علي الرغم من فكرة تعالق الجسيمات الثلاثة وتعديلات فرضية جون بل تواصل تسميتها GHZ.
ويمكن لنسق الجسيمات الثلاثة في عرض فرضية GHZ إما أن يكون تعديلا لتجربة حركة دورانية أو استقطاب، أو يمكن أن يكون تعديلاً لتعالق شعاع.
ومن أكثر الأمور غرابة حول تعالق الجسيمات الثلاثة، والسبب الرئيسي للاهتمام الذي لقيه طرح GHZ ، أنه يمكن استخدامه في إثبات فرضية جون بل بدون المعالجات المرهقة للمتباينات.
ومازال السؤال مطروحا : كيف يمكن إجراء تعالق لثلاثة فوتونات في المعمل؟ فهذا أمر لا يمكن تحقيقه إلا من خلال خاصية كمية محيرة حقا، كما تم توضيحه من خلال ما طرحه زايلنجر وشركاؤه العاملون معه عام ١٩٩٧ . وثمة توضيح في الشكل التالي.
لنفرض وجود زوجين من الفوتونات المتعالقة ضمن تجهيزات تجريبية معينة تجعل عنصرا من أحد الزوجين يتعذر تمييزه عن عنصر آخر من الزوج الثاني، وتم احتجاز فوتون واحد من الفوتونين اللذين لم يتم تمييزهما، تغدو الفوتونات الثلاثة المتبقية متعالقة. وما لا يمكن تصديقه هنا أن الفوتونات أصبحت متعالقة لأن مراقبا خارجيا لا يستطيع أن يحدد الزوج الذي أنتج الفوتون المحتجز. ثم، إذا نحينا جانبا الفوتون المحتجز، لتعالقت الفوتونات الثلاثة المتبقية. وقد استطاع زايلنجر ومعانوه إنتاج هذا النسق فعليا عام ١٩٩٩.
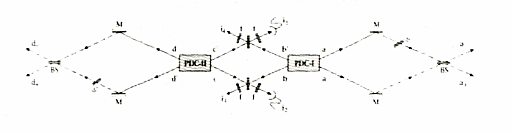
وثمة كتابات تتناول برهان GHZ فرضية جون بل باستخدام ،فوتونات ،الثلاثة .المتعالقة. إذ يعرضها كل من دافيد ميرمين، ومجموعة GHZ أنفسهم، وكذلك في كتاب صدر مؤخرا لدانيال ستير Daniel Styer وفيها معالجات بأشكال مناسبة ككتاب مدرسي.
ويسهل التوصل إلي هذه المعالجات لسببين مشتركين: الأول: أن التنبؤات الكمية لا تعتمد علي الاشتقاقات بل يتم ببساطة تقديم وصف لها، لذلك فإنها تعفي القارئ من معرفة المشتقات الرياضية. والثاني: لا يتم وصف كل التنبؤات الكمية، بل لا يحدث ذلك إلا للتنبؤات التي تحتاج إلي معالجة. والتعديل التالي أجراه مايك هورن، واستخدمه في مايو 2001 في محاضرته البحثية المميزة التي قدمها في كلية ستونهيل كولدج ولطلابها . وهذا التعديل يستعير الكثير من المعالجات المبكرة، مع التبسيط الإضافي الذي يستخدم تعديل GHZ لتعالق الشعاع، وبالتالي يتجنب الحركة الدورانية أو الاستقطاب. وتم اقتباس هذه المعالجة من محاضرة مايك بموافقة كريمة من مؤلفها وبمساعدته.
يوضح الشكل التالي تجهيزات تجربة GHZ للشعاع المتعالق، وهي بوضوح تعميم مباشر لقياس تداخل جسيمين ليصبح ثلاثة جسيمات. توضع مرأة نصف مفضفضة عند كل موضع من المواضع الثلاثة لتتخذ أحد وضعين، إما الوضع الأيسر ( L) ، أو الوضع الأيمن (R) . وتتغير نتائج التجربة تبعا لهذه الأوضاع.
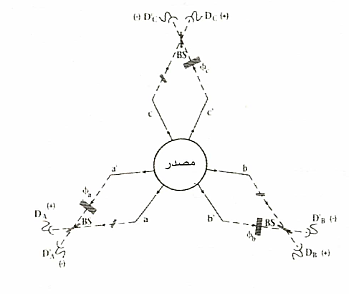
ويوضح الشكل نسقا يوجد به مصدر من نوع خاص جدا في المركز يبث ثلاثة جسيمات متعالقة في أن واحد ونظرا لأن هذه الجسيمات (أو الفوتونات) هي أجسام كمية، كما أنها متعالقة، فإن كل "ثلاثي جسيمي يمر من الفتحاتc, b, a ، معا وكذلك خلال الفتحات'c, 'b, 'a ، ولأنها تمر عن طريق تصميم الماسة الثلاثية، فإن كل جسيم يصطدم بمقسم أشعة (مرأة نصف مفضضة)، يمكن أن تتخذ الوضع L أو الوضعR .
وتتنبأ ميكانيكا الكم بأنه لكل جسيم تحدث النتائج أما +1 أما - ١ (التي تناظر الحركة الدورانية "لأعلى" أو "لأسفل" للجسيم، أو اتجاه الاستقطاب الرأسي أو الأفقي للفوتون) للترددات المتساوية: وتكون في نصف الزمن +١، وفي نصف الزمن - ١ ، بصرف النظر عن مواقع مقسمات الشعاع. وذا نظرنا إلي أزواج الفوتونات، فمازلنا لا نري أي شكل مثير للانتباه: فكل أزواج النتائج (+1 ،+1)،(-1، -1)، (+1، -1)، (- ١ ، +1) سوف تحدث مع التردد المتساوي (الزمن لكل منها) لكلا الجسيمين A ،B (وبالطريقة نفسها للأزواج الأخرى)، بصرف النظر عن مواقع مقسمات الشعاع. ومع ذلك تتنبأ ميكانيكا الكم أن أي ملاحظ سيري رقصا سحريا فعليا إذا تعين عليه أن ينظر لما يحدث للجسيمات الثلاثة جميعها . وعلي سبيل المثال، تتنبأ ميكانيكا الكم أنه إذا كان مقسما الشعاع للجسيمين Bو C كلاهما في الوضع L، كما استقر هذان الجسيمان، مثلا، علي كواشف النتيجة - ١، وذا كان مقسم الشعاع A في الوضع R، إذن لاستقر بالتأكيد الجسيم؟علي الكاشف +1. وهذا تنبؤ ملحوظ بدرجة قوية، كما توجد تنبؤات متقنة مماثلة للتوليفات الأخرى للأوضاع. ويعرض الجدول التالي ملخصا لهذه العمليات ولتنبؤات ميكانيكا الكم.

ثمة عمليات توليف أخري مثل LLL لا نحتاج إليها في هذا العرض.
والتنبؤات المذكورة على يسار الجدول لعمليات التوحيد في يمين الجدول حصل عليها كل من جرينبرجر وشيموني وزايلنجر باستخدام رياضيات ميكانيكا الكم. وبطبيعة الحال، فقد بدأوا بحالة التعالق الفعلية للجسيمات الثلاثة. وفكرة التعالق هي عملية تراكب للحالات، كما نعرف، وبالنسبة لثلاثة جسيمات يمر كل منها خلال فتحتين، نحصل علي حالة تراكب يمكن كتابتها (على نحو ما بالصيغة المبسطة)علي الصورة:
(a' b' c' + a b c)
وهذه المعادلة هي الصيغة الرياضية لتعالق الجسيمات الثلاثة، وفيها العلامة "+" تحتجز الاثنين -.
ومن هذه المعادلة، التي تصف عملية تراكب الحالات - بمعني، تقدم وصفا رياضيا يطابق تماما ما هو المقصود بتعالق ثلاثة جسيمات، ضمن إطار الترتيب الخاص لهذه التجربة التي تحتوي علي ست فتحات. استنبط الفيزيائيون الرياضيات واشتقوا التنبؤات المدونة في الجدول السابق- ويمكن الحصول علي التفصيلات الفعلية من ملحق الورقة "فرضية حون بل بدور متباينات" التي كتبها كل من جرينبرجر، وهورن، وشيموني، وزايلنجر، في العدد 58 بتاريخ ١٢ ديسمبر1990 من المجلة الأمريكية للفيزياء، American Journal of Physics. وينبغي ملاحظة أنه حتي في ورقتهم العلمية، فإن المؤلفين قد أحالوا الاشتقاق الجبري - لتنبؤات الميكانيكية الكمية والتي تعتمد علي معادلة الحالة - إلي ملحق، وكان ملحقا مطولا إلى حد بالغ، وهو عنصر أساسي في ميكانيكا الكم. ويمكن للقارئ المهتم (المتمكن من الرياضيات) أن يتابع هذه التفاصيل في الملحق. والأمر المهم الذي يتعين علي القارئ فهمه هو أن التنبؤات المدونة بالجدول أعلاه تتفق على نحو تام مع ما تقول لنا ميكانيكا الكم إنه سيحدث في كل حالة. ولا يوجد المزيد في هذه التنبؤات أكثر من تطبيق قواعد ميكانيكا الكم علي نسق معين وعلى حالة التعالق. للجسيمات الثلاثة. ولذلك سنأخذ هذه التنبؤات باعتبارها نتائج صحيحة ومباشرة لتعالق ثلاثة جسيمات.
وإذا عدنا إلي جدولنا عن التنبؤات الميكانيكية الكمية لحالة تعالق الجسيمات الثلاثة، نجد أنه: بفرض معرفة أوضاع مقسم الشعاع، وبفرض معرفة النتائج المعينة للجسيم B والجسيم C، فإن ما يحدث للجسيمA قابل للتنبؤ علي نحو موثوق. وعلي سبيل المثال، نفرض أن مقسمي الشعاع للجسيمين B و C كلاهما في الوضع 1 ، وأن الجسيمB يستقر في الكاشف -١ ، وكذلك C في - ١ . إذن إذا كان مقسم شعاع الجسيمA في الوضع R، فإن الجسيم A سيذهب بالتأكيد إلي الكاشف1+ . وثمة معاملات ارتباط تامة مماثلة - كما يلاحظ من الجدول السابق- لخيارات أخري لأوضاع مقسم الشعاع والنتائج الأخرى في موقعين. وباختصار، بفرض معرفة أوضاع مقسم الشعاع والنتائج المعينة للجسيمين BوC ، فإن نتيجة الجسيمA قابلة للتنبؤ على نحو مؤكد.