The internal energy
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص30-33
2025-11-01
50
The internal energy
In thermodynamics, the total energy of a system is called its internal energy, U. The internal energy is the total kinetic and potential energy of the molecules in the system (see Comment 1.3for the definitions of kinetic and potential energy).1We denote by ∆Uthe change in internal energy when a system changes from an initial state i with internal energy Ui to a final state f of internal energy , Uf: ∆U=Uf−Ui , The internal energy is a state function in the sense that its value depends only on the current state of the system and is independent of how that state has been prepared. In other words, it is a function of the properties that determine the current state of the system. Changing any one of the state variables, such as the pressure, results in a change in internal energy. The internal energy is an extensive property. That the internal energy is a state function has consequences of the greatest importance, as we start to unfold in Section 2.10. Internal energy, heat, and work are all measured in the same units, the joule (J). The joule, which is named after the nineteenth-century scientist J.P. Joule, is defined as 1 J = 1 kg m2 s−2 , A joule is quite a small unit of energy: for instance, each beat of the human heart consumes about 1 J. Changes in molar internal energy, ∆Um, are typically expressed in kilojoules per mole (kJ mol−1). Certain other energy units are also used, but are more common in fields other than thermodynamics. Thus, 1 electronvolt (1 eV) is defined as the kinetic energy acquired when an electron is accelerated from rest through a potential difference of 1 V; the relation between electronvolts and joules is 1 eV ≈ 0.16 aJ (where 1 aJ = 10−18 J). Many processes in chemistry have an energy of several electronvolts. Thus, the energy to remove an electron from a sodium atom is close to 5 eV. Calories (cal) and kilocalories (kcal) are still encountered. The current definition of the calorie in terms of joules is
1 cal = 4.184 J exactly , An energy of 1 cal is enough to raise the temperature of 1 g of water by 1°C.
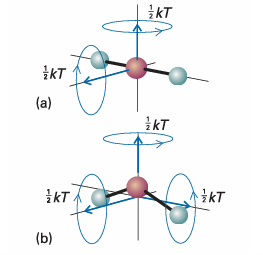
Fig. 2.5The rotational modes of molecules and the corresponding average energies at a temperature T. (a) A linear molecule can rotate about two axes perpendicular to the line of the atoms. (b) A nonlinear molecule can rotate about three perpendicular axes. It has been found experimentally that the internal energy of a system may be changed either by doing work on the system or by heating it. Whereas we may know how the energy transfer has occurred (because we can see if a weight has been raised or lowered in the surroundings, indicating transfer of energy by doing work, or if ice has melted in the surroundings, indicating transfer of energy as heat), the system is blind to the mode employed. Heat and work are equivalent ways of changing a system’s internal energy. A system is like a bank: it accepts deposits in either currency, but stores its reserves as internal energy. It is also found experimentally that, if a system is isolated from its surroundings, then no change in internal energy takes place. This summary of observations is now known as the First Law of thermodynamics and expressed as follows: The internal energy of an isolated system is constant. We cannot use a system to do work, leave it isolated for a month, and then come back expecting to find it restored to its original state and ready to do the same work again. The evidence for this property is that no ‘perpetual motion machine’ (a machine that does work without consuming fuel or some other source of energy) has ever been built. These remarks may be summarized as follows. If we write w for the work done on a system, q for the energy transferred as heat to a system, and ∆U for the resulting change in internal energy, then it follows that ∆U= q+w (2.2) , Equation 2.2 is the mathematical statement of the First Law, for it summarizes the equivalence of heat and work and the fact that the internal energy is constant in an isolated system (for which q = 0 and w = 0). The equation states that the change in internal energy of a closed system is equal to the energy that passes through its bound ary as heat or work. It employs the ‘acquisitive convention’, in which w > 0 or q > 0 if energy is transferred to the system as work or heat and w < 0 or q < 0 if energy is lost from the system as work or heat. In other words, we view the flow of energy as work or heat from the system’s perspective.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
