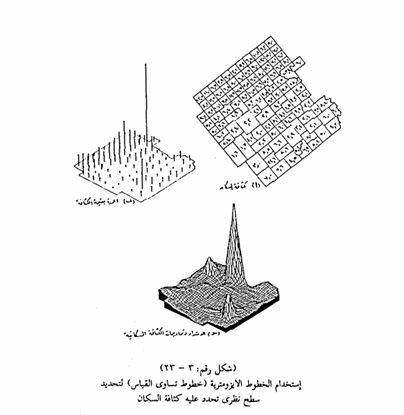
إذا كانت البيانات المراد تمثيلها بيانات ذات مدى عظيم في القيم أو الكميات فإننا ندخل البعد الثالث الذي  يترتب عليه استخدام أشكال بيانيه حجمية تتناسب في أحجامها مع مقدار الكميات التي تمثلها ومن أهم هذه الأشكال الحجمية الذي يعرف باسم الشكل البياني أو المجسم المنظوري Isometric Block Diagram وهو الرسم الذي يعتمد على رسم نوع من خطوط التساوى تعرف بخطوط الايزومتر تساوي القياس التي يتطابق مفهوما مع مفهوم خطوط الايزوبلث، والتي تظهر تموجات السطوح الاحصائية التي يعتمد تحديدها على قيم مشتقة لا يمكن أن توجد عن مواقع معينة مثل قيم كثافة السكان التي تتعرض ملازم كبير نوعا فيما يختص بالموقع والفرق بين خط الايزومتر وخط الايزويلث هو في اواقع عبارة عن محاولة للتمييز بين نوعيم من الخطوط يختلفان في دقة تحديدهما للسطوح الاحصائية، أكثر منها محاولة للتمييز بين أنواع من الرموز الكارتوجرافية ، كما أن خطوط الايزومترز هي في الأصل تبين توزيع القيم الحقيقية المطلقة، وتوزيع القيم المشتقة التي يمكن أن توجد عند مواقع مثل مؤشر التركيب العمري للسكان، ومن هنا تسمى خطوط التساوي التي ترسم لها الغرض باسم خطوط الايزومتر للتركيب العمري Isometric Lines of Age true ture. وخطوط الايزومتر في هذه الحالة تقدم لنا صورة إجمالية لتموجات و اختلافات السطح الاحصائي Statistical surface ، مثل الصورة التي توضح شكل الأرض بارتفاعاته وانحداراته، كما أنها تمثل أسلوبا مبتكرا لتصوير سلسلة من القيم الكمية تصويرا بيانيا يخدم كخطوط هيئة أو شكل مجرد تحديد مرتفعات وانخفاضات السطح الاحصائى أكثر منها خطوط لتصوير قيم حقيقية واضحة التحديد عند نقطة معينة.

وعندما نصمم شكليات بيانيا من نوع الايزومتر الذي يمثل تموجات السطح الإحصائي، فلا مناص من تحدد السطح الاحصائي بعدد محدود من القيم، بحيث نستنتج من هذه القيم المحدودة المجموع الكلي الذي يحدد السطح الاحصائي. وبعد ذلك نوقع نقطة القيم على مسافة ما من بعضها على الرسم، ثم ندخل عليها خطوط التساوي التي لابد أن تمثل لنا في العناية سطحا احصائيا مستمرا.

وصفوة القول أنه يمكن استخدام الخطوط الايزومترية لتحديد سطح نظرى أو معنوي مثل السطح الذي نحدد عليه كثافة السكان، وفي هذه الحالة تصبح قيم لتجديد عبارة عن معدلات أي متوسط عدد الأشخاص في كل متر مربع مثلا ولنضرب مثالا يوضح طريقة التمثيل بخطوط التساوي الأيزو مترية فإذا كانت دينا بيانات من كثافة السكان في منطقة ما موقعه في منتصف كل وحدة إدارية منها فإننا نقوم بتحويلها إلى شكل بياني - أي بإقامة أعمدة على كل وحدة يتناسب طولها مع الكمية التي يمثلها ويمكن بعد ذلك توضيح هذا الشكل بطريقة أخرى تبين نفس التوزيع ولكن بصورة أخرى لا تظهر شكل السطح بأبعاده الثلاثة فحسب، بل توضح بعض الخصائص المتمثلة في الامتداد إلى جانب اختلافات تموجات الكثافة السكانية على أنه يمكن اعتبار أن الشكل الأخرى تمثيلا لسطح احصائى يتكون من سلسلة من القيم المتوسطة التي تتصف بأن لها ثلاثة أبعاد(س، ص، ع) للوحدات المساحية المختارة. حيث تمثل (س)، (ص) الامتداد الأفقى للوحدة المساحية، بينما تمثل (ع) الارتفاع النسبي المفترض الذي يكون فوق أو تحت منسوب أفقى معين يسمى مستوى المقارنة Datum  ولما كانت كل وحدة مساحية هنا تمثل مجموعا كبيرا أو صغيرا من القيم النقطية، فليس هناك نقطة مفردة يمكن أن تكون لها لهذه القيمة المتوسطة (كثافة السكان) ومع ذلك فمن الضروري في مثل هذه الحالة أن تفترض أو ندعي وجود مثل هذه القيم المتوسطة عند نقطة مفردة إذا أردنا أن تمثل تموجات هذا السطح الاحصائي بخطوط التساوى الايزومترية.

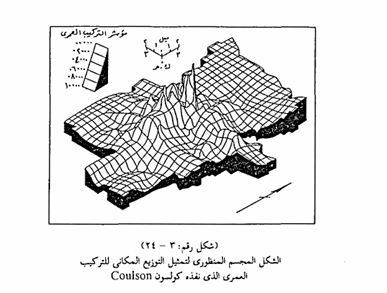
ومن أشهر الأمثلة لتطبيق مثل هذه الأشكال لتمثيل بيانات السكان ما قام به کونسون Coulson من حساب مؤشر للتركيب العمري للسكان كمقياس منفرد يعبر عن خصائص التركيب العمرى للسكان. كما قام برسم هیستو جرام مثالي للتركيب العمرى ومنه أسس علاقة خطية بين مجموعات فئات السن المتباينة، ثم بعد ذلك حسبت معدلات خط الانحدار لمجموعة صغار السن والتي أعطت نتائج دلت على شدة انحدار خط العلاقة، بينما قل انحدار خط هذه العلاقة كثيرا المجموعة كبارالسن. وباستخدام هذا المؤشر فقد أصبح في الامكان تمثيل التوزيع المكاني للتركيب العمري بطرق متباينة والتي منها الشكل المجسم المنظوري Isometric block-doagram والذي ينتج عن سطح مأخوذ من خريطة تتمثل فيها بيانات توزيع مكاني للتركيب العمري بخطوط التساوى اعتمادا على مؤشر التركيب العمري.

وحسبنا هنا على الجملة أن تقول أن تمثيل السطح ذي الأبعاد الثلاثة يتضمن أصعب مشاكل التمثيل الكارتوجرافي ، ولهذا فقد خصص لها الكارتوجرافيون من دراساتهم وجهودهم أكثر ما خصصوه لكل مشكلات الرموز الكارتوجرافية الأخرى مجتمعة وبالرغم من ذلك فقد شاع استخدام الأشكال البيانية التوضيحية لتمثيل التوزيع الجغرافي ذي الأبعاد الثلاثة عن طريق الصورة الى نحدد فيها سطح هذا التوزيع في التحليل الجغرافي الذي يعتمد على النماذج الوصفية للتناسق المكاني. فعلى سبيل المثال أصبح في الأماكن وعن طريق تنفيذ السطح ذي الأبعاد الثلاثة، ومن الشكل الهندسى لهذا السطح أن نستدل على امتداد الحجم الجغرافي للظاهرة القائم على مستوى الأساس الذي قد نفترضه نحن، وذلك لبيان المنشآت الصناعية في منطقة معينة، أو الاختلافات في كثافة السكان أو الاختلاف في معدلات النمو.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم شؤون المعارف يصدر كتابًا قرآنيًّا بعنوان (كن فيكون)

قسم التطوير يقيم دورة تدريبية عن مهارات الإلقاء والتواصل الفعال لعددٍ من ملاكات العتبة العباسية المقدسة

قسم الشؤون الفكرية يقيم دورة في مجال ترميم المخطوطات والوثائق لطلبة جامعة الكوفة

المجمع العلمي يواصل إقامة أنشطته القرآنية في مختلف المحافظات العراقية

المزيد

الآخبار الصحية

أول إرشادات غذائية قائمة على الأدلة لمعالجة الإمساك المزمن

صباح بلا إفطار؟.. صحتك في خطر!

هل يمكن للجلد أن يكشف عن صحتك العقلية؟.. دراسة حديثة تجيب

السر في مطبخك.. 6 أطعمة تمنح عظامك قوة الشباب

المزيد

الآخبار التكنلوجية

ناسا تكشف: كوكب الأرض أصبح أقل لمعانا خلال العقود الماضية

دراسة: الوقت الذي تستخدم فيه هاتفك قد يفضح حالتك النفسية

الهنغاري لاسلو كراسناهوركاي يفوز بجائزة نوبل للآداب 2025

رسميا.. إعلان الفائز بجائزة نوبل للسلام لعام 2025

المزيد

مواضيع ذات صلة

الهرم السكاني البسيط

الأهرامات السكانية المركبة Compound Pyramids

الدين وديمغرافية السكان

توزيع السكان في اوربا

السكان في أوروبا

تركيب السكان

السكان وتوزيعهم في ليبيا

النشاط البشري في قارة افريقيا

السكان في اقليم غرب افريقيا

التوزيع السكاني لقارة افريقيا

السكان في افريقيا

سنغافورة