Symmetry operations, elements and point groups

Key points: Symmetry operations are actions that leave the molecule apparently unchanged; each symmetry operation is associated with a symmetry element. The point group of a molecule is identified by noting its symmetry elements and comparing these elements with the elements that define each group. A fundamental concept of the chemical application of group theory is the symmetry operation, an action, such as rotation through a certain angle, that leaves the molecule apparently unchanged. An example is the rotation of an H₂O molecule by 180º around the bisector of the HOH angle (Fig. 6.1). Associated with each symmetry operation there is a symmetry element, a point, line, or plane with respect to which the symmetry operation is performed. Table 6.1 lists the most important symmetry operations and their corresponding elements. All these operations leave at least one point unchanged (the centre of the molecule), and hence they are referred to as the operations of point-group symmetry. The identity operation, E, consists of doing nothing to the molecule. Every molecule has at least this operation and some have only this operation, so we need it if we are to classify all molecules according to their symmetry. The rotation of an H₂O molecule by 180º around a line bisecting the HOH angle (as in Fig. 6.1) is a symmetry operation, denoted C₂. In general, an n-fold rotation is a symmetry operation if the molecule appears unchanged after rotation by 360º/n. The corresponding symmetry element is a line, an n-fold rotation axis, Cn, about which the rotation is per formed. There is only one rotation operation associated with a C₂ axis (as in H₂O) because clockwise and anticlockwise rotations by 180º are identical. The trigonal-pyramidal NH₃  

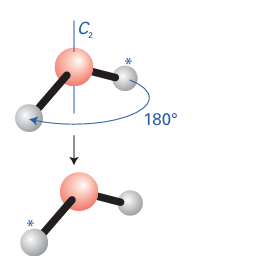
Figure 6.1 An H₂O molecule may be rotated through any angle about the bisector of the HOH bond angle, but only a rotation of 180 (the C2 operation) leaves it apparently unchanged.

molecule has a threefold rotation axis, denoted C₃, but there are now two operations associated with this axis, one a clockwise rotation by 120º and the other an anticlockwise rotation by 120º (Fig. 6.2). The two operations are denoted C₃ and C₃² (because two successive clock wise rotations by 120º are equivalent to an anticlockwise rotation by 120º), respectively.

The reflection of an H₂O molecule in either of the two planes shown in Fig. 6.4 is a symmetry operation; the corresponding symmetry element, the plane of the mirror, is a mirror plane, Ϭ.

The H₂O molecule has two mirror planes that intersect at the bisector of the HOH angle. Because the planes are ‘vertical’, in the sense of containing the rotational (z) axis of the molecule, they are labelled with a subscript v, as in Ϭ_v and Ϭ_v . The XeF₄ molecule in Fig. 6.3 has a mirror plane h in the plane of the molecule.

The subscript h signifies that the plane is ‘horizontal’ in the sense that the vertical principal rotational axis of the molecule is perpendicular to it. This molecule also has two more sets of two mirror planes that intersect the fourfold axis. The symmetry elements (and the associated operations) are denoted Ϭ_v for the planes that pass through the F atoms and Ϭ_d for the planes that bisect the angle between the F atoms. The d denotes ‘dihedral’ and signifies that the plane bisects the angle between two C₂ axes (the FXeF axes).

To understand the inversion operation, i, we need to imagine that each atom is projected in a straight line through a single point located at the centre of the molecule and then out to an equal distance on the other side (Fig. 6.5). In an octahedral molecule such as SF₆, with the point at the centre of the molecule, diametrically opposite pairs of atoms at the corners of the octahedron are interchanged. The symmetry element, the point through

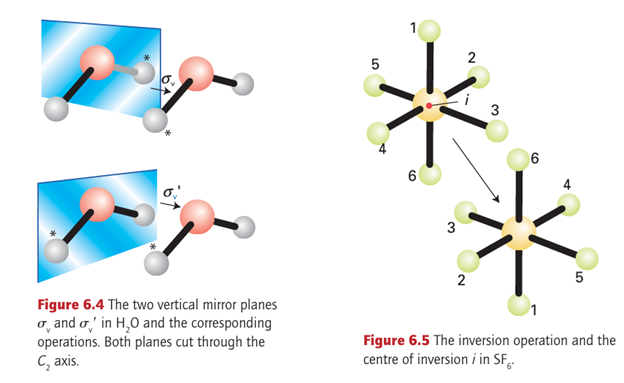
which the projections are made, is called the centre of inversion, i. For SF₆, the centre of inversion lies at the nucleus of the S atom. Likewise, the molecule CO₂ has an inversion centre at the C nucleus. However, there need not be an atom at the centre of inversion: an N₂ molecule has a centre of inversion midway between the two nitrogen nuclei. An H₂O molecule does not possess a centre of inversion. No tetrahedral molecule has a centre of inversion. Although an inversion and a twofold rotation may sometimes achieve the same effect, that is not the case in general and the two operations must be distinguished (Fig. 6.6).

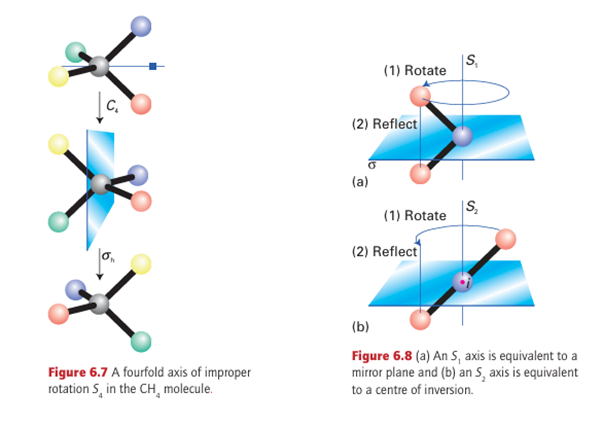
An improper rotation consists of a rotation of the molecule through a certain angle around an axis followed by a reflection in the plane perpendicular to that axis (Fig. 6.7). The illustration shows a fourfold improper rotation of a CH4 molecule. In this case, the operation consists of a 90º (that is, 360°/4) rotation about an axis bisect ing two HCH bond angles, followed by a reflection through a plane perpendicular to the rotation axis. Neither the 90º (C4) operation nor the reflection alone is a symmetry operation for CH₄ but their overall effect is a symmetry operation. A fourfold improper rotation is denoted S₄. The symmetry element, the improper-rotation axis, Sn (S₄ in the example), is the corresponding combination of an n-fold rotational axis and a perpendicular mirror plane.

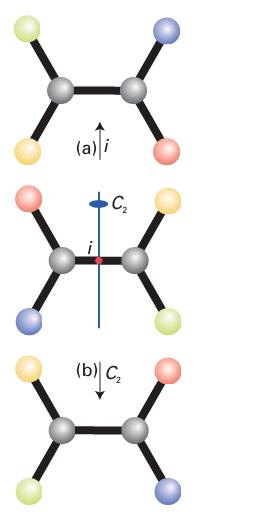
Figure 6.6 Care must be taken not to confuse (a) an inversion operation with (b) a twofold rotation. Although the two operations may sometimes appear to have the same effect, that is not the case in general.

اخر الاخبار

اخبار العتبة العباسية المقدسة

في علوم نهج البلاغة العتبة العباسية المقدسة تطلق مشروع بناء الإنسان وتقويم اللسان

قسم الصيانة يواصل أعمال البنى التحتية في مشروع استراحة الواحة على طريق (النجف - كربلاء)

جامعة الكفيل تختتم دورة تدريبية مخصصة لتنمية المهارات وتعزيز الانضباط الوظيفي

المجمع العلمي يجري اختباره للمتقدمين على قناة حفظة القرآن الكريم في النجف الأشرف

المزيد

الآخبار الصحية

هل يمكن الاعتماد على "ChatGPT" في الحصول على نصائح صحية؟

قبل أي نشاط رياضي.. هذه الفاكهة ينصح بها الخبراء

استخدام القنب للعلاج.. دراسة تحذر من من "جنون العظمة" ؟!

غالبية الناس ينظفون أسنانهم خطأ.. إليك الطريقة الصحيحة

المزيد

الآخبار التكنلوجية

نصائح لإطالة عمر بطارية السيارة وضمان أدائها الأمثل

الرياض تحتضن مونديال الرياضات الإلكترونية بدعم stc

"ستارشيب" ينطلق في رحلة تجريبية ويسقط بالمحيط الهندي !

شركة جديدة.. خطة ماسك لمنافسة مايكروسوفت في الذكاء الاصطناعي

المزيد

مواضيع ذات صلة

The stability field of water

Standard potentials and spontaneity

Heterogeneous acid–base reactions

Superacids and superbases

Acidic and neutral solvents

Basic solvents

Solvents as acids and bases

Interpretation of hardness

The classification of acids and bases

Halogens as Lewis acids

Group 14 Lewis acids

Group 13 Lewis acids