Now, of course, we can put our definition of temperature into Eq. (39.9) and so find the law for the pressure of gases as a function of the temperature: it is that the pressure times the volume is equal to the total number of atoms times the universal constant k, times the temperature:

Furthermore, at the same temperature and pressure and volume, the number of atoms is determined; it too is a universal constant! So equal volumes of different gases, at the same pressure and temperature, have the same number of molecules, because of Newton’s laws. That is an amazing conclusion!

In practice, when dealing with molecules, because the numbers are so large, the chemists have artificially chosen a specific number, a very large number, and called it something else. They have a number which they call a mole. A mole is merely a handy number. Why they did not choose 10²⁴ objects, so it would come out even, is a historical question. They happened to choose, for the convenient number of objects on which they standardize, N₀=6.02×10²³ objects, and this is called a mole of objects. So instead of measuring the number of molecules in units, they measure in terms of numbers of moles. ³ In terms of N₀ we can write the number of moles, times the number of atoms in a mole, times kT, and if we want to, we can take the number of atoms in a mole times k, which is a mole’s worth of k, and call it something else, and we do—we call it R. A mole’s worth of k is 8.317 joules: R=N₀k=8.317 J⋅mole−1⋅^∘K−1. Thus we also find the gas law written as the number of moles (also called N) times RT, or the number of atoms, times kT:

It is the same thing, just a different scale for measuring numbers. We use 1 as a unit, and chemists use 6×10²³ as a unit!

We now make one more remark about our gas law, and that has to do with the law for objects other than monatomic molecules. We have dealt only with the CM motion of the atoms of a monatomic gas. What happens if there are forces present? First, consider the case that the piston is held by a horizontal spring, and there are forces on it. The exchange of jiggling motion between atoms and piston at any moment does not depend on where the piston is at that moment, of course. The equilibrium conditions are the same. No matter where the piston is, its speed of motion must be such that it passes energy to the molecules in just the right way. So it makes no difference about the spring. The speed at which the piston has to move, on the average, is the same. So our theorem, that the mean value of the kinetic energy in one direction is 1/2 kT, is true whether there are forces present or not.

Consider, for example, a diatomic molecule composed of atoms m_A and m_B. What we have proved is that the motion of the CM of part A and that of part B are such that ⟨1/2 m_Av²_A⟩=⟨1/2 m_Bv²_B⟩=3/2 kT. How can this be, if they are held together? Although they are held together, when they are spinning and turning in there, when something hits them, exchanging energy with them, the only thing that counts is how fast they are moving. That alone determines how fast they exchange energy in collisions. At the particular instant, the force is not an essential point. Therefore, the same principle is right, even when there are forces.

Let us prove, finally, that the gas law is consistent also with a disregard of the internal motion. We did not really include the internal motions before; we just treated a monatomic gas. But we shall now show that an entire object, considered as a single body of total mass M, has a velocity of the CM such that

In other words, we can consider either the separate pieces or the whole thing! Let us see the reason for that: The mass of the diatomic molecule is M=m_A+m_B, and the velocity of the center of mass is equal to v_CM=(m_Av_A+m_Bv_B)/M. Now we need ⟨v²_CM⟩. If we square v_CM, we get

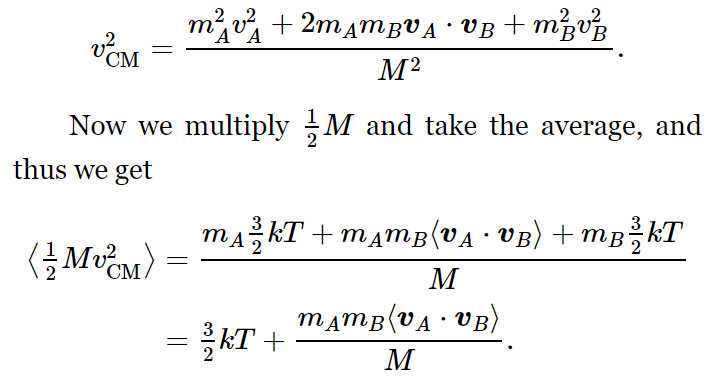
 (We have used the fact that (m_A+m_B)/M=1.) Now what is ⟨v_A⋅v_B⟩? (It had better be zero!) To find out, let us use our assumption that the relative velocity, w=v_A−v_B is not any more likely to point in one direction than in another—that is, that its average component in any direction is zero. Thus, we assume that

Therefore, since ⟨m_Av²_A⟩=⟨m_Bv²_B⟩, the first and last terms cancel out on the average, and we are left with

Thus if m_A≠m_B, we find that ⟨v_A⋅v_B⟩=0, and therefore that the bodily motion of the entire molecule, regarded as a single particle of mass M, has a kinetic energy, on the average, equal to 3/2 kT.

Incidentally, we have also proved at the same time that the average kinetic energy of the internal motions of the diatomic molecule, disregarding the bodily motion of the CM, is 3/2 kT! For, the total kinetic energy of the parts of the molecule is 1/2 m_Av²_A+1/2 m_Bv²_B, whose average is 3/2 kT+3/2 kT, or 3kT. The kinetic energy of the center-of-mass motion is 3/2 kT, so the average kinetic energy of the rotational and vibratory motions of the two atoms inside the molecule is the difference, 3/2 kT.

The theorem concerning the average energy of the CM motion is general: for any object considered as a whole, with forces present or no, for every independent direction of motion that there is, the average kinetic energy in that motion is 1/2 kT. These “independent directions of motion” are sometimes called the degrees of freedom of the system. The number of degrees of freedom of a molecule composed of r atoms is 3r, since each atom needs three coordinates to define its position. The entire kinetic energy of the molecule can be expressed either as the sum of the kinetic energies of the separate atoms, or as the sum of the kinetic energy of the CM motion plus the kinetic energy of the internal motions. The latter can sometimes be expressed as a sum of rotational kinetic energy of the molecule and vibrational energy, but this is an approximation. Our theorem, applied to the r-atom molecule, says that the molecule will have, on the average, 3rkT/2 joules of kinetic energy, of which 3/2 kT is kinetic energy of the center-of-mass motion of the entire molecule, and the rest, 3/2 (r−1)kT, is internal vibrational and rotational kinetic energy.

________________________________________________________
Margin

3- What the chemists call molecular weights are the masses in grams of a mole of a molecule. The mole is defined so that the mass of a mole of carbon atoms of isotope 12 (i.e., having 6 protons and 6 neutrons in the nucleus) is exactly 12 grams.

مواضيع ذات صلة

Evaporation

Evaporation of a liquid

Temperature and kinetic energy

Compressibility of radiation

The pressure of a gas

Properties of matter

Matter is made of atoms

تحول المادة إلى طاقة

GAS PRESSURE

GASES IN OUTER SPACE

GASES NEAR A PLANET

DIFFUSION IN SMALL CONTAINERS