
الانحراف المعياري Standard Deviation
 المؤلف:
أ. د محمد مجدي واصل
المؤلف:
أ. د محمد مجدي واصل
 المصدر:
اسس الكيمياء التحليلية
المصدر:
اسس الكيمياء التحليلية
 الجزء والصفحة:
ص 40-43
الجزء والصفحة:
ص 40-43
 2023-09-13
2023-09-13
 2541
2541
وهو أكثر مقاييس التشتت شيوعاً ، واستعمالاً ، ولحسابه نلجأ الي مقياس آخر من مقاييس التشتت يدعى التباين ، والتباين هو متوسط مربعات انحرافات قيم النتائج المتحصل عليها عن الوسط الحسابي لها . فإذا كانت القيم ,X1 2, X3,X .... مجموعة من المشاهدات وسطها الحسابي فإن يمثل مجموع مربعات انحرافات القيم عن وسطها الحسابي ، وعند ذلك يمكن حساب التباين الذي يرمز له بالرمز δ2 ( سيجما تربيع ) من العلاقة التالية :
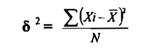
والانحراف المعياري هو الجزر التربيعي للتباين ويرمز له بالرمز
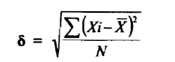
حيث تستخدم هذه العلاقة إذا كان عدد القراءات (N) كبيراً جداً ، ويفوق الثلاثين أما إذا كان عدد القراءات أقل من 30 فإن الإنحراف المعياري يعطي من قراءة العلاقة
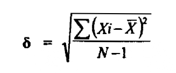
حيث N-1 هي عبارة عن درجات الحرية Degrees of Freedom
مثال (3) :
احسب قيمه الانحراف المعياري للنتائج التالية : 20,19,18,10,15,14

مثال (4(
في تحليل محتوي عينة صخرية من كوبونات الكالسيوم CaCO3 سجلت النتائج التالية 60 , 65 ، 70 ، 73 ، 80 ، 75 ، 64 ، 70 % أوجد من ذلك المدى ، والانحراف المعياري المتوسط ، والانحراف المعياري .
الحل :
من الجدير بالذكر أن هناك اصطلاحين هامين في المعالجات الإحصائية للنتائج هما الدقة Accuracy والأحكام precision وتعرف دقة قراءة ما بأنها مقدار تباعد القراءة عن القيمة الحقيقية ، كما يقدر الإحكام بتباعد قراءة المشاهدة عن متوسط كافة القراءات
ويجب ملاحظة الفارق الكبير ما بين الدقة والإحكام، حيث إن الدقة تقارن القيمة المأخوذة بالقيمة المقبولة ، وأما الإحكام فهو يقارن القراءة بقراءة أخري ، أخذت بنفس الظروف وبنفس الطريقة التي أخذت بها القراءة الأولي الدقة في القراءة غالباً ما توضع على شكل الخطأ المطلق ورياضياً
E=Xi-Xt
حيث أن الخطأ المطلق ( E ) هو عبارة عن الفرق بين القيمة المشاهدة ( Xi ) والقيمة المقبولة ( Xt ) .
مثال (5 (
في تجربة لتحديد النسبة المئوية للكلوريد في عينة ما سجلت النتائج التالية :-
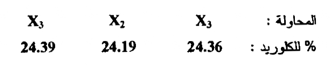
فإذا علمت أن العينة تحتوي على 24.36% كلوريداً ، فأوجد الخطأ المطلق المتوسط الحسابي .
الحل :
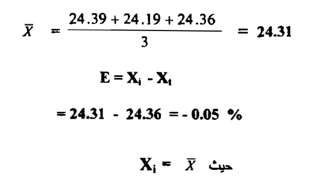
والإشارة السالبة هنا تعني أن المتوسط الحسابي ، أو المشاهدة أقل من القيمة المقبولة ، أما إذا كانت الإشارة موجبة فهذا يعني أن القراءة أعلي من القيمة المقبولة ، ويكون الخطأ النسبي مساوياً
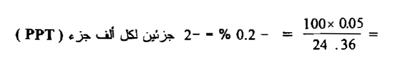
 الاكثر قراءة في مواضيع عامة في الكيمياء التحليلية
الاكثر قراءة في مواضيع عامة في الكيمياء التحليلية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


