Cardinal Exponentiation
المؤلف:
Ciesielski, K
المصدر:
Set Theory for the Working Mathematician. Cambridge, England: Cambridge University Press, 1997.
الجزء والصفحة:
...
26-12-2021
1026
Cardinal Exponentiation
Let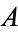 
and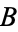 
be any sets, and let 
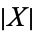be the cardinal number of a set 
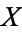. Then cardinal exponentiation is defined by
(Ciesielski 1997, p. 68; Dauben 1990, p. 174; Moore 1982, p. 37; Rubin 1967, p. 275, Suppes 1972, p. 116).
It is easy to show that the cardinal number of the power set of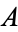 
is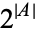 
, since ![|<span style=]()
{0,1}|=2" src="https://mathworld.wolfram.com/images/equations/CardinalExponentiation/Inline7.gif" style="height:16px; width:59px" /> and there is a natural bijection between the subsets of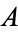 
and the functions from 
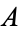into ![<span style=]()
{0,1}" src="https://mathworld.wolfram.com/images/equations/CardinalExponentiation/Inline10.gif" style="height:16px; width:30px" />.
REFERENCES:
Ciesielski, K. Set Theory for the Working Mathematician. Cambridge, England: Cambridge University Press, 1997.
Dauben, J. W. Georg Cantor: His Mathematics and Philosophy of the Infinite. Princeton, NJ: Princeton University Press, 1990.
Moore, G. H. Zermelo's Axiom of Choice: Its Origin, Development, and Influence. New York: Springer-Verlag, 1982.
Rubin, J. E. Set Theory for the Mathematician. New York: Holden-Day, 1967.
Suppes, P. Axiomatic Set Theory. New York: Dover, 1972.
الاكثر قراءة في نظرية المجموعات
اخر الاخبار
اخبار العتبة العباسية المقدسة
