Let a distribution to be approximated be the distribution 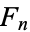 of standardized sums

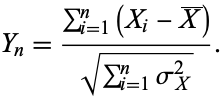(1)

In the Charlier series, take the component random variables identically distributed with mean 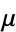, variance 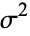, and higher cumulants  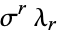for 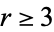. Also, take the developing function  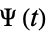as the standard normal distribution function 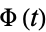, so we have

			(2)
			(3)
			(4)

Then the Edgeworth series is obtained by collecting terms to obtain the asymptotic expansion of the characteristic function of the form

(5)

where 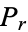 is a polynomial of degree  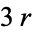with coefficients depending on the cumulants of orders 3 to 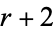. If the powers of  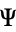are interpreted as derivatives, then the distribution function expansion is given by

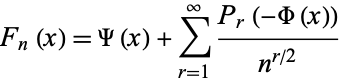(6)

(Wallace 1958). The first few terms of this expansion are then given by

(7)

Cramér (1928) proved that this series is uniformly valid in .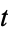

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 935, 1972.

Charlier, C. V. L. "Über dir Darstellung willkürlicher Funktionen." Ark. Mat. Astr. och Fys. 2, No. 20, 1-35, 1906.

Cramér, H. "On the Composition of Elementary Errors." Skand. Aktuarietidskr. 11, 13-74 and 141-180, 1928.

Edgeworth, F. Y. "The Law of Error." Cambridge Philos. Soc. 20, 36-66 and 113-141, 1905.

Esseen, C. G. "Fourier Analysis of Distribution Functions." Acta Math. 77, 1-125, 1945.

Hsu, P. L. "The Approximate Distribution of the Mean and Variance of a Sample of Independent Variables." Ann. Math. Stat. 16, 1-29, 1945.

Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, pp. 107-108, 1951.

Wallace, D. L. "Asymptotic Approximations to Distributions." Ann. Math. Stat. 29, 635-654, 1958.