Random Walk--2-Dimensional
المؤلف:
McCrea, W. H. and Whipple, F. J. W.
المصدر:
"Random Paths in Two and Three Dimensions." Proc. Roy. Soc. Edinburgh 60
الجزء والصفحة:
281-298
24-3-2021
2278
Random Walk--2-Dimensional
In a plane, consider a sum of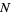 
two-dimensional vectors with random orientations. Use phasor notation, and let the phase of each vector be random. Assume 
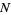unit steps are taken in an arbitrary direction (i.e., with the angle 
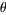uniformly distributed in 
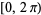and not on a lattice), as illustrated above. The position 
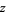in the complex plane after 
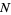steps is then given by
 |
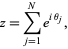(1)
|
which has absolute square
Therefore,
 |
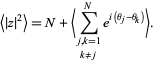(5)
|
Each unit step is equally likely to be in any direction (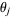
and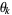 
). The displacements are random variables with identical means of zero, and their difference is also a random variable. Averaging over this distribution, which has equally likely positive and negative values yields an expectation value of 0, so
 |
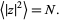(6)
|
The root-mean-square distance after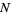 
unit steps is therefore
 |
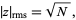(7)
|
so with a step size of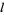 
, this becomes
 |
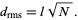(8)
|
In order to travel a distance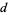 
,
 |
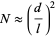(9)
|
steps are therefore required.
Amazingly, it has been proven that on a two-dimensional lattice, a random walk has unity probability of reaching any point (including the starting point) as the number of steps approaches infinity.
REFERENCES:
McCrea, W. H. and Whipple, F. J. W. "Random Paths in Two and Three Dimensions." Proc. Roy. Soc. Edinburgh 60, 281-298, 1940.
الاكثر قراءة في الاحتمالات و الاحصاء
اخر الاخبار
اخبار العتبة العباسية المقدسة
