Interval Stationary Point Process
المؤلف:
Daley, D. J. and Vere-Jones, D.
المصدر:
An Introduction to the Theory of Point Processes Volume I: Elementary Theory and Methods, 2nd ed. New York: Springer, 2003.
الجزء والصفحة:
...
10-3-2021
2065
Interval Stationary Point Process
A point process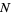 
on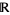 
is said to be interval stationary if for every 
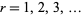and for all integers 
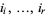, the joint distribution of
![<span style=]() {tau_(i_1+k),...,tau_(i_r+k)} " src="https://mathworld.wolfram.com/images/equations/IntervalStationaryPointProcess/NumberedEquation1.gif" style="height:21px; width:95px" /> |
does not depend on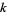 
, 
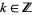. Here, 
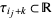is an interval for all 
.
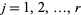As pointed out in a variety of literature (e.g., Daley and Vere-Jones 2002, pp 45-46), the notion of an interval stationary point process is intimately connected to (though fundamentally different from) the idea of a stationary point process in the Borel set sense of the term. Worth noting, too, is the difference between interval stationarity and other notions such as simple/crude stationarity.
Though it has been done, it is more difficult to extend to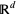 
the notion of interval stationarity; doing so requires a significant amount of additional machinery and reflects, overall, the significantly-increased structural complexity of higher-dimensional Euclidean spaces (Daley and Vere-Jones 2007).
REFERENCES:
Daley, D. J. and Vere-Jones, D. An Introduction to the Theory of Point Processes Volume I: Elementary Theory and Methods, 2nd ed. New York: Springer, 2003.
Daley, D. J. and Vere-Jones, D. An Introduction to the Theory of Point Processes Volume II: General Theory and Structure, 2nd ed. New York: Springer, 2007.
الاكثر قراءة في الاحتمالات و الاحصاء
اخر الاخبار
اخبار العتبة العباسية المقدسة
